Quantitative Analysis: Some Pointers

When it comes to counsellors and psychotherapists, everyone hates stats. Well, almost everyone. Aside from a few geeks like myself who would prefer nothing better than sitting in front of an Excel spreadsheet for days.

…Oh yes: and, then, there’s also the funders, commissioners, and policy-makers who all rely almost exclusively on the statistical analysis of data. And that creates a real tension. Most of us don’t come into therapy to do statistical analysis. We want to engage with people—real people—and studying people and processes by numbers can feel like the most de-humanising, over-generalising kind of reductionism. But, on the other hand, if we want to have an impact on the field and influence policy and practice, then we do need to engage with quantitative, statistical analysis. Or, at least, understand what it is saying and showing. If not, there’s a danger that those therapies that are most humanistic and anti-reductionistic are also those that are most likely to get side-lined in the world of psychological therapy delivery.

And there is also another, less polarised, way of looking at this. From a pluralistic standpoint, no research method—like no approach to therapy—is either wholly ‘right’ or ‘wrong’ (see our recent publication on pluralistic research here). Rather, different methods of research and analysis are helping in asking different questions at different points in time. So if you are asking, for instance, about the average cost of a therapeutic intervention; or whether, on average, a client is more likely to find Therapy A or Therapy B more helpful; then it does make sense to use statistics. (But if you wanted to know, for instance, how different clients experienced Therapy A, then you’d be much better off using qualitative methods).

This blog presents a very basic introduction to terms and concepts in quantitative analysis. This may be helpful if you are wanting to present some basic statistical analyses in a research paper, or if you are reading quantitative research papers and want to get more of a grasp on what they are meaning and doing. You can find many books and guides on the internet that give more in-depth introductions to quantitative analysis, one of the most popular being Andy Field’s Discovering Statistics Using IBM SPSS Statistics.

Quantitative analysis and statistical analysis are essentially the same thing (and will be used synonymously in this blog): the analysis of number-based data. The principle alternative to quantitative analysis is qualitative analysis, which refers to the analysis of language-based data.

Descriptive Statistics

There are two main sorts of quantitative analysis. The first is descriptive statistics. This is where numbers are used to show what a set of data looks like (as opposed to testing particular hypotheses, which we’ll come on to). Descriptive statistics may be used in a Results section to present the findings of a study but, even if you are doing a qualitative study, you may use some descriptive statistics to present some data about your participants. So always worth knowing.

Frequencies

Probably the most basic statistic is just saying how many of something there are: for instance, how many participants you had in a study, or how many of them were BAME/White/etc. There are two basic ways to do this:

• Count. ‘There were nine participants in the study; three of them were of a black or minority ethnicity and six were white.’ Count is just the number of something, and about as simple as statistics gets.

• Percentage. Percentage is the amount of something you would have if there was 100 in total. It’s a way of standardising counts so that we can compare them. For instance, if we had three BAME participants out of nine total participants in one study; and ten BAME participants out of 1000 total participants in a second study; the count of BAME participants in the second study is higher, but actually they were more representative in the former. We work out percentages by dividing the count we’re interested by the total count, then multiplying by 100. So our percentage in the first study is 3/9 * 100 (‘/’ means ‘divide by’, ‘*’ means ‘multiply by’), which is 33.3%; and in our second study is 10/1000 * 100, which is 1%. 33.3% vs. 1%: that really shows us a meaningful difference in representation across the two studies. Percentages are easy to work out by Excel: just do a formula where you divide the number in the group of interest by the total number, and multiple by 100. Only do percentages when it’s needed though: that is, when it would be hard for the reader to work out the proportion otherwise. With small samples (less than ten or so) you probably don’t need it. If we had, for instance, one White and one BAME participant, it’s a bit patronising to be told that there’s 50% of each!

Averages

One way of pulling together a large set of numerical data is through averages. This is a way of combining lots of bits of data to give some indication of what the data, overall, looks like. There are three main types of averages:

• Mean. This is the one that you come across most frequently, and is generally the most accurate representation of the middle point in a set of data. The mean is the mathematical average, and is worked out by adding up all the scores in a set of data and then dividing by the number of data points. For instance, if you had three young people who scores on the YP-CORE measure of psychological distress (which ranges from 0 to 40, with higher scores meaning more distress) were 10, 15, and 18, then we could work out the mean by adding the scores together (which gives us 43) and then dividing by the number of scores (which is 3). So the mean is 43/3 = 14.3. Whenever we have several bits of data along the same scale—for instance ages of participants in a study, or scores of participants on a measure of the alliance—it can be useful to combine it together using the mean. Means are easy to do on Excel using the function AVERAGE. Note, don’t worry about lots and lots of decimal points. Really, for instance, that the mean above is 14.3333333333333333333333333 etc but no-one needs to know that level of detail. It just looks like we are trying to be clever and actually makes it harder for the reader to know what is going on! So normally one decimal point is enough (unless the number is typically less than 1.0, in which case you could give a couple of decimal points).

• Median. Sometimes our data might have an usual distribution. Supposing, for instance, that we did a study and our participants ages were 20, 22, 23, 24, and 95. Well, the mean here would be 36.8 years old, but it doesn’t seem to describe our data very well because we have one ‘outlier’ (the 95 year old) who is very different from the other participants. So an alternative kind of average is the median, which is where we line up our values in a consecutive sequence, and then identify the middle. In this instance, we have five values and the middle one is 23 years old. The MEDIAN function on Excel is also very easy to use, and is a useful way of describing our data when there isn’t too much of it or it’s not smoothly spread out. If the mean and median of a set of values are very different, it’s normally helpful to give both—less important if they are virtually the same.

• Mode. Let’s be frank, the mode is like the useless youngest sibling of the central tendency family: it doesn’t really tell you much and doesn’t get used very often. The mode is just the most common response. So, for instance, if we had YP-CORE scores of 20, 20, 23, 25, and 40 the mode would be 20 because there are two of those scores and one of every other one. Not much use, huh! But some times it can be quite informative. For instance, it’s an interesting fact that the modal number of sessions attended at many therapy services is 1. So even though the mode and median may be closer to 6 or so sessions, it’s interesting to note that the most common number of sessions attended is much less. MODE can be shown in Excel, but only report it if it adds something meaningful to what you are presenting.

Spread

Say you had a group of people who were aged 20, 30, and 40 years old. Then you had a second group that were aged 29, 30, and 31 years old. If we just gave the mean or the median of the groups, they’d actually be the same: 30 years old. But, clearly, the two sets of data are a bit different, because the first one is more spread out than the second one. So, if we want to understand a dataset as comprehensively as possible, with as few as possible figures, then we also need some indication of spread.

• Range. The range is the simplest way of giving an indication of the spread of a dataset, and just means giving the highest and lowest values. So, for instance, with the first dataset above you might say: ‘Mean = 30 years old, range = 20-40 years old’. That can be pretty informative, though for larger datasets the highest and lowest numbers don’t tell us much about what is in the middle.

• Standard deviation. The standard deviation, or SD, is an indication of the spread of a dataset. In contrast to the frequencies or central tendencies, it’s not a number that intuitively means much, but it’s essentially the average amount that the values in a dataset vary from the mean. So in the first group above, the standard deviation is 10 years and in the second group it’s 1 year. Essentially, a higher standard deviation means more spread. Pretty much always, if you’re giving a mean you’ll also want to give the standard deviation; so, in a paper, you’ll see something like: ‘Mean = 30 years old (SD = 10)’. Means look pretty naked without an SD. But it’s not easy to work out yourself, and you’ll need to use something like Excel that can calculate it using the function STDEV.

• Standard error. This is getting a bit more complicated, and you’re unlikely to need standard error (SE) if you’re just presenting some simple descriptive statistics, but it is worth knowing about because it’s the basis for a lot of subsequent analyses. Let’s say we’re interested in the levels of psychological distress of young people coming in to school counselling, and we use the YP-CORE to measure it. We get an average level of 20.8 and a standard deviation of 6.4 (this is what we actually got in our ETHOS study of school-based counselling). So far so good. But, of course, this is just one sample of young people in counselling, and what we really want to know is what the average levels of distress of all young people coming into counselling is: the population mean (so sample is the group we are studying, and population is everyone as a whole). So how good is our mean of 20.8 at predicting what the population mean might actually be? OK, so here’s a question: if that mean came from a sample of 10,000 young people, or if it came from a sample of five young people, which would give the most accurate indicator of the population mean (all other things being equal)? Answer (I hope you got this), from the sample of 10,000 people. Why? Because in the sample of five young people, any individual idiosyncrasies could really influence the mean; whereas in a much larger sample these are likely to get ironed out. So the standard error is an indication of how much the sample mean is likely to vary from the true population mean, and it’s worked out by dividing the standard deviation by the sample size (square-rooted). Don’t worry about why it’s the square root (the number that, when multiplied by itself, gives that value—for instance the square root of nine is three). But it just means that the larger a sample, the smaller the standard error gets: indicating that it varies around the true population mean by a smaller amount. Phew!

• Confidence intervals. Again, the standard error, as a statistic, isn’t a number that intuitively means much. One thing that is often done with it, however, is to work out the confidence intervals around a particular mean. The confidence interval is our guestimate of where the true population mean is likely to lie, given our sample mean. And it’s always at a particular level of confidence, normally 95% (or sometimes 99%). So if you see something like ‘Mean YP-CORE score = 20.8, 95%CI = 19.5 - 22.1)’ it’s telling us that we can be 95% certain that the true population mean for YP-CORE scores of young people coming into counselling is between 19.5 and 22.1. Pretty cool, and confidence intervals are used more and more these days, because there’s a move from pretending we know precisely what a population mean is to being more cautious in suggesting whereabouts it might lie. Confidence intervals aren’t too difficult to calculate—for 95% CIs, you add, and take away, 1.96 * the standard error—but, like standard errors, there’s no automatic way of doing it on Excel: you need to set up the formula yourself. Or use more sophisticated statistical analysis software like IBM SPSS. Why 1.96? There’s a very good reason, but for that you need to look at one of the more in-depth introductions to stats. 

effect sizes

Effect sizes are a really good statistic to know about when you are reading research papers, because they are one of the most commonly reported statistics these days. Also, if you are wanting to compare anything statistically—for instance, whether boys or girls have higher levels of distress when they come into counselling—you’ll want to be giving an effect size.

In fact, there are hundreds and hundreds of different effect size statistics. An effect size is just an indicator of the magnitude of a relationship between two variables. So that might be gender and levels of psychological distress, or it might be the relationship between the number of sessions of art therapy and subsequent ratings of satisfaction. Whatever effect size statistics is used, though, the higher it is the stronger the relationship between two variables.

• Cohen’s d. The most common form of effect size that you see in the therapy research literature is Cohen’s d, or some variant of it (for instance, ‘Hedges’s g’ or the ‘standardised mean difference’). This is used to indicate the difference between two groups on some variable. For instance, we could use it to indicate the amount of difference in levels of psychological distress for boys and girls coming into counselling, or to indicate how much difference counselling made to young people’s levels of psychological distress as compared with care as usual (which is what we did in our ETHOS study). Cohen’s d is basically the amount of difference between two scores divided by their standard deviations. So, for instance, if boys had a mean level of distress on the YP-CORE of 20, and girls had a mean of 22, and the standard deviation across the two groups was 4.0, then we would have an effect size of 0.5. (This is the difference between 22 and 20 (i.e., 2 points) divided by 4.0). Dividing the raw difference in scores by the standard deviation is important because if, for instance, boys’ and girls’ scores varied very markedly already (i.e., a larger standard deviation), then a difference of 2 points between the two groups would be less meaningful than if the differences in scores were otherwise very small. Typically, when we interpret effect sizes like Cohen’s d:

  • 0.2 = a small effect

  • 0.5 = a medium effect

  • 0.8 = a large effect

  So we could say that there is a medium difference between girls and boys when coming into counselling. In our study of humanistic counselling schools, we found an effect size of 0.25 on YP-CORE scores after 12-weeks between the young people who had counselling and those who didn’t, suggesting that the counselling had a small effect. We can also put a confidence interval around that effect size, for instance ours was 0.03 to 0.47, indicating that we were 95% confident that the true effect of our intervention on young people would lie somewhere between those two figures.

correlational analyses

Correlations are, actually, another form of effect size. But they specifically tell us about the size of relationship between linear variables (i.e., where the scores vary along a numerical scale, like age or YP-CORE scores) rather than between a linear variable and categorical variable (i.e., where there are different types of things, like White vs. BAME, or counselling vs. no counselling).

• Correlations. These are used to indicate the magnitude of relationship between just two linear variables. It’s a number that ranges from -1 to 0 to +1. A negative correlation indicates that, as one number goes up the other goes down. So, for instance, a correlation of -.8 between age and levels of psychological distress would indicate that, as children get older, their levels of distress go down. A correlation of 0 would indicate that these two variables weren’t related in any way. A positive number would indicate that, as children get older, so they are more distressed. Correlations can be easily calculated on Excel using the function CORREL. Typically, in interpreting correlations

  • 0.1 = a small association

  • 0.3 = a medium association

  • 0.5 = a large association

Tables

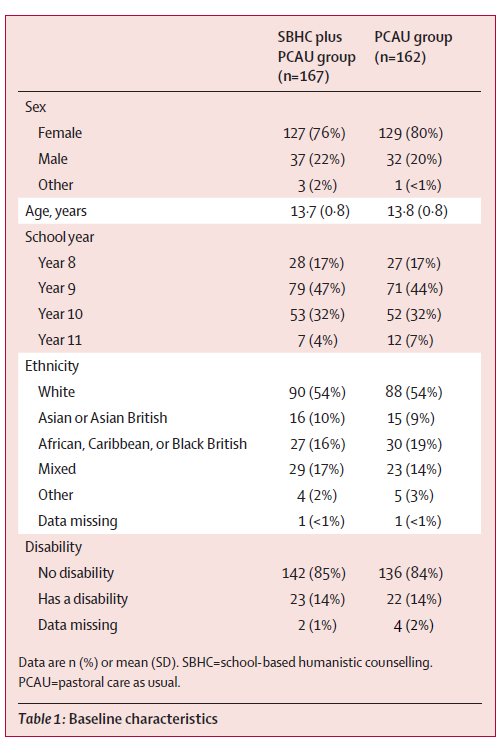
If you’ve got lots of different bits of quantitative data (say six or more means/SDs), it’s generally good to present it in a table. Below, for instance, is a table that we used to present data from our ETHOS study about young people who had school-based humanistic counselling plus pastoral care as usual (SBHC plus PCAU group) and those who had pastoral care as usual alone (PCAU group).

In our text, we also gave a narrative account of the main details here (for instance, how many females and males) but the table allowed us to present a lot of detail that we didn’t need to talk the reader through. Generally, tables are a better way of presenting the data than figures, such as graphs, because they can more precisely convey the information to a reader (for instance, a reader won’t know the decimal points from a graph). Just to add, if you are doing a table of participant demographics, the format above is a pretty good way to do it, with different characteristics listed in the left hand column, grouped under subheadings (like ‘Disability’). That works even when there’s just one group, and is generally better than trying to do different characteristics across the top.

Graphs

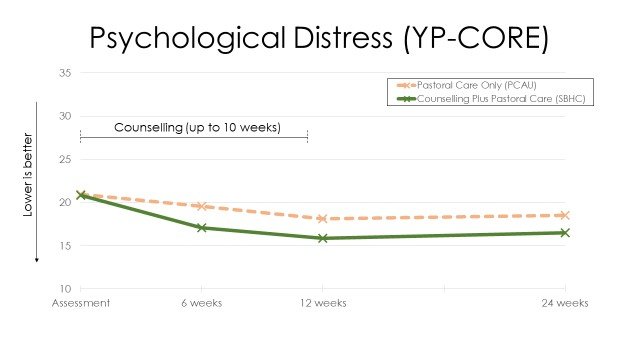
…But graphs do look prettier, and sometimes they can communicate key relationships between variables that a table or narrative might not. For instance, below is a graph showing our ETHOS results that gives a pretty clear picture of how our two groups changed on our key outcome measure of psychological distress over time. This gives a very immediate representation of what our findings were, and can be particularly useful when conveying results to a lay audience. However, for an academic audience, graphs can be relatively imprecise: if you wanted to know the exact scores, you’d need to get a ruler out! So use graphs sparingly in your own reports and only when they really convey something that can’t be said in a table. And I’d generally say NAAPC (nearly always avoid pie charts): you can get some lovely colours in them, but they take up lots of space and don’t tend to communicate that much information.

Main outcomes from the ETHOS study

Inferential Statistics

Basic principles

So now we come on to the second main type of quantitative analysis: inferential statistics. This is where we use numbers to test hypotheses: that is, we’re not just describing the data here but trying to test particular beliefs and assumptions. Inferential statistics are notoriously difficult to get your head around, so let’s start by taking a step back and thinking about the problem that they’re trying to solve.

Let’s say we find that, after 10 weeks of dramatherapy, older adults have a mean score of 15 on the PHQ-9 measure of depression, while those who didn’t participate in dramatherapy have a mean score of 16. Higher scores on the PHQ-9 mean more depression, but is this difference really meaningful? What, for instance, if those who had dramatherapy had mean scores of 15.9, as opposed to 16.0 for those without—what would we make of that? The problem is, there’s always going to be some random variations between groups—for instance, one might start off with more depressed people—so any small differences between outcomes might be due to that. So how can we say, for instance, whether a difference of 0.1 points between groups is meaningful, or a difference of 1 point, or a difference of 10 points? What we’re asking here, essentially, is whether the differences we have found between our samples are just a result of random variations, or whether they reflect real differences in the population means. That is, in the real world, overall, does dramatherapy actually bring about more reductions in depression for older adults?

So here’s what we can do, and it’s a pretty brilliant—albeit somewhat quirky, on first hearing—solution to this problem. Let’s take our difference of 1 point on the PHQ-9 between our dramatherapy and our no dramatherapy groups. Now, we can never say, for sure, whether this 1 point difference does reflect a real population difference/effect, because there’s always the possibility that our results are due to random variations in sampling. But what we can do is to work out the probability that the difference we have found is simply due to random variations in sampling. The way we do this is by saying, ‘If there were no real differences between the two groups (the null hypothesis), how likely is it that we would have got this result?’ For instance, ‘If dramatherapy was not effective at all, how likely is it that we would have got a 1 point difference between the two groups?’ We can work that out basically by looking at the ratio between how much scores tend to vary anyway across people (i.e., the standard deviation), and then how much they vary between the two specific groups. For instance, if we find lots of differences in how older adults score on the PHQ-9 after therapy, and only very small differences between those who had, and did not have, dramatherapy, the likelihood that the mean differences between the two groups would be due to just random variations would be fairly high. The exact method to calculate this ratio is beyond this blog (and Excel too—you generally need proper statistical software), but the key figure that comes out of it all is a probability value, or p-value. So this is a number, from 1.0 downwards, which tells you how likely it is that your results are just due to chance. So you might get a p-value of .27 (which means that there is a 27% likelihood that your results were due to chance) or .001 (which means that there is a 0.1%, one-in-a-thousand, likelihood that it was due to chance).

So what do you do with that? Well, the standard procedure is to set a cut off point and to say that, if our probability-value is less than that, we’ll say that our difference is significant. That cut-off point is typically .05 (i.e., 1-in-20), and sometimes .01 (i.e., 1-in-100). So, essentially, what we do is to see whether the probability of our results coming about by random is 1-in-20 or less and, if it is, we say that we have a significant result. Why 1-in-20? Well, that’s a bit random in itself, but it’s an established norm, and pretty much any paper you see will use that cut off point to assess whether the likelihood is so low that we’re going to say we’ve found a meaningful difference. Note, if we don’t find a p-value of less than 1-in-20 we can’t say that we’ve shown two things are the same. For instance, if our p-value for dramatherapy against no dramatherapy was 0.27, it doesn’t prove that dramatherapy is no more effective than no dramatherapy. It just means that, at this point, we can’t claim that we have found a significant difference.

Statistical tests

There are a large number of statistical tests that you’ll see in the literature, all based on the principles outlined above. That is, they all ways of looking at different sets of data and asking the question, ‘How likely is it that these results came about by chance?’ If it’s less than 1-in-20, then the null hypothesis that the results are just due to random variations is rejected, and a significant finding is claimed. That’s what researchers are looking for; and it’s a bit weird because, as you can see, what we’re trying to do is to disprove something we never really believed in in the first place! It’s all based, though, around the principle that you can only ever disprove things, not prove things—see Karl Popper’s work on falsifiability here.

Some of the most common families of statistical tests you will come across are:

• T-tests. These are the most simple tests, and compare the means of two groups. This may be ‘between-participants’ (for instance, PHQ-9 scores for people who have dramatherapy, and those who do not have therapy) or ‘within-participants’ (for instance, PHQ-9 scores for people at the start of dramatherapy, and then at the end).

• Analysis of variance (ANOVAs). These are a family of tests that compare scores across two or more different groups. For instance, the PHQ-9 scores of participants in dramatherapy, counselling, and acupuncture could be compared against each other. Multiple analyses of variance allows you to compare scores on different dimensions, and then also the interactions between the different dimensions. For instance, an experimental study might look at the outcomes of these three different interventions, and then also compare short term and long term formats. Repeated measures analyses of variance combine within- and between-participant analyses: comparing, for instance, changes on the PHQ-9 from start of therapy to end of therapy for clients in dramatherapy, as compared with one or more other interventions.

• Correlational tests. Correlations (see above), like differences in means, are very rarely exactly 0, so how do we know if they are meaningful or not? Again, we can use statistical testing to generate a p-value, indicating how likely the association we find is due to random chance.

• Regression analysis. Regression analysis is an extension of correlational testing. It is a way of looking at the relationship between one linear variable (for instance, psychological distress) and a whole host of other linear variables at the same time (for instance, age, income level, psychological mindedness). Categorical variables, like gender or ethnicity, can also be entered into regression analyses by converting them into linear variables (for instance, White becomes a 1 for ‘yes’, and a 0 for ‘no’). So regression analyses allow you to look at the effects of lots of different factors all at once, and to work out which ones are actually predictive of the outcome and which are not. For instance, correlational tests may show that both age and ethnicity are associated with higher levels of distress, but a regression analysis might indicate that, in fact, age effects are cancelled out once ethnicity is accounted for.

• Chi-squared tests. As we’ve seen, some data, like gender or diagnoses, is primarily categorical: meaning that it exists in different types/clumps, rather than along continua. So if we’re asking a question like, ‘Are there differences in the extent to which boys and girls are diagnosed with ADHD vs depression?’, we can’t use standard linear-based tests, because there’s no outcome variable. Instead, we use something called a chi-squared test, which is specifically aimed at looking at differences across frequency counts.

… And that’s just the beginning. There’s a mind-boggling number of further tests, like structural equation modelling, cross-panel lag analysis, multilevel modelling, and a whole family of non-parametric tests, but hopefully that gives you a rough idea. There all different procedures, but they’re all based around the same principle: How likely is it, given the results that you got, that there is no difference between the groups? If that likelihood is less than 1-in-20, we’re going to say that something ‘significant’ is going on.

Final thoughts

Whether you like stats or not, they’re there in the research, so if you want to know something of what the research says, you do need to have a basic understanding of them. But we don’t need to get into either/or about it. Stats have their strengths and they have their limitations: from a pluralistic standpoint, they tell one (very helpful at times) story, but it’s not the only story that tells us what’s going on.

Stats, to some extent at least, is also changing. When I trained as a psychology undergraduate in the 1980s, for instance, it was all about significant testing. Today, particularly in psychotherapy research, there’s more emphasis on using stats descriptively, in particular effect sizes and confidence intervals. That’s through a recognition that the kind of yes/no answers you get from inferential tests are too binary and too unrepresentative of the real world.

If you’re staring blankly at this blog and thinking, ‘What the hell was that about?’ do let me know in the comments what wasn’t clear and I’ll try and explain it better. I do, I guess, wish the therapy world would love stats a bit more. I guess that’s partly because it’s so important for understanding what’s getting commissioned and funded and making a difference there; but maybe more because I can see, for myself, so much beauty in it. And that doesn’t in any way take away from the beauty of words or language or art or the many, many other ways of knowing. But numbers can also have a very special place there in helping us to understand people and therapy more; and once you’ve got a basic grasp of what they are trying to do, hopefully they’ll feel more like friend than foe.

Acknowledgements

Photo by Mick Haupt on Unsplash

Disclaimer

 The information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

The ‘Research Mindset’: Some Pointers

After years of supervising—and teaching—Master’s and doctoral research students in counselling, psychotherapy, and counselling psychology, there’s one thing that, I’ve come to believe, is the key to success. It’s hard to describe, but goes something like this….

When you study or research at undergraduate level, it’s all about showing how much you know. You have to convince your assessors that you are ‘up to it’: that you know enough to meet the learning outcomes for that award.

Students often approach Master’s or doctoral research with the same mindset: they want to show how much they know, that they’re doing it the right way, that they understand the process and the content of the research that they are conducting.

For Master’s and doctoral research that is, indeed, still important; but there is also something much more. When you do research at this level, you are moving from being a student to being a teacher. You, now, are the one who knows. And what the academic community, including your examiners, want from you is not so much to test you or to check your knowledge in a particular field, but to learn from you. We’re looking to you to tell us about what you’re discovering because you know more than us. Yes, that’s right. You do (or, at least, will do); and you need to be able to own that authority.

This can be a hard one: ‘Who am I, I’m just a student, how am I supposed to know anything special?’ But, at doctoral (and to some extent Master’s) level, you are, by definition, being asked to make an original and significant contribution at the leading edge of your field. So, to some extent, this shift needs to happen whether you like it or not. You need to be the big person in the room.

Is this about being arrogant? No, of course not. Is it about pretending you know everything? No, not that either. Is it about patronising your supervisors or your examiners? Definitely not, no. What it is about is being confident and secure in your knowledge and feeling that you have something to educate others about—something to even the most senior figures in the field.

Because the reality is, you do. If you’re researching at Master’s or doctoral level, you should be focusing on a question that no-one else, or very few other people, have ever asked. And that does make you the expert. You know more than us. You know more than your supervisors, you know more than your examiners. You know more than other people in the academic field. And what’s really important to recognise is that we want to learn from you. When someone agrees to examine you for your viva, for instance, or when they come to see you present your research at a conference, they’re not thinking, ‘Mm, I’ve always wondered whether [insert your name here] is good enough for a Master’s/doctoral degree’, or, ‘I’ve always thought [insert your name here] is really just pretending to know things, and I’m now going to find out for sure.’ Nope, that’s probably the last things on their minds. Rather, a large part of the reason they’ve agreed to spend two days reading your thesis and then travelling to your university to examine you, etcetera, is because they’re interested in what you’ve discovered and want to find out more. After all (and apologies to the narcissists here) would anyone really want to spend two or more days of their life just checking up on you? In a world where everyone is so furiously busy what people mostly want is to learn, as effectively and efficiently, what you know so that they can inform and develop their own work and ideas. We want to learn from you.

Doing it despite

Of course that can be scary. When we start off learning in any field, we are inevitably novices; and some of us have ‘imposter syndrome’ throughout our careers. That’s totally understandable. But researching at doctoral and Master’s level means being and doing something despite these fears. It means holding, and owning, our knowledge, skills, and expertise. So if you find it difficult to own that teacher role, this might be something useful to take to therapy: ‘Why is it so difficult for me to see myself as an authority here?’ It gets to the very heart of who we are and how we feel about ourselves.

A key to researching and writing

Although this ‘teacher mindset’ is relatively hard to describe; once you can get into it, it can really unlock the research and writing up process. It means you can write with confidence; and with balance, because you know that what you are saying is important, and that people are wanting a serious, reflective, critical commentary from you. And it means that you are likely to avoid some of the pitfalls stemming from a wholly ‘student mindset’. One problem you sometimes see in students’ theses, for instance, is that their Discussion says next to nothing about their own findings—it focuses solely on the research and theory introduced in their Literature Review. Why does that happen? Probably because, to some extent, the student doesn’t really believe that their own findings have much to say: so they just skip over it and back to the ‘important stuff’. Get into that teacher mindset, however, and you’ll find that you naturally take your own findings much more seriously: they’re not just some throw-away bits of data, they’re carefully curated evidence that have a meaning and significance to the wider field of knowledge.

Narrowing down your focus

One key thing in getting to be—and feeling like—the expert is ensuring that the scope of your research is sufficiently narrow. If you take on a massive area, like ‘the effectiveness of therapy’, you’re never going to feel like (or, indeed, be) the leading authority in that area. There’s people who have spent their lifetimes researching this, carried out hundreds of studies, so, of course, you are going to feel less knowledgeable than them. But if you narrow down your focus—for instance, ‘the effectiveness of compassion-focused therapy (CFT) for health anxiety’—then, immediately, the number of leading authorities in the field dramatically reduces. Sure, people might know about the overall effectiveness of CFT more than you, or the processes by which it supports change; but when it comes to CFT for health anxiety, you’re likely to be in a field of one. And that’s when everyone starts to turn to you to discover what you’ve found, because you’re then genuinely contributing to the knowledge-base. So if you’re feeling like you could never ‘hold’ that expert position in your field, it may be worth looking at how broad your field is. You can, I promise, get to that expertise level, but it is very dependent on the breadth of the question you are asking.

Against authority

But is it OK to be an ‘authority’? Perhaps another block to that teacher mindset, for those of us from more humanistic and person-centred orientations, is that we’re wary of taking on too dominant a role: we don’t like to position ourselves as ‘better’ than others. Here, equality, respect, treating the other as like ourselves are all the principal values. Yes, absolutely; but recognising that we know more than others in one particular field isn’t saying we’re better or smarter than others. We can know lots and others can know lots as well; and if we all share our specialist knowledges—and dialogue between them—then we can all make contributions to a better world for all. Equality doesn’t have to mean sameness. Indeed, recognising our own special knowledges—and giving that away to others—can be part of a world that celebrates difference, diversity, and uniqueness for all.

facing the unknowable

To adopt that teacher mindset, you also have to be willing to face the unknowability of a lot of the questions you are asking. At school and at undergraduate level, the questions you were asked had ‘right’ answers—or, at least, your teachers and lecturers told you they did. Multiple choice questions make it clear that there are ‘rights’ and ‘wrongs’. But when you’re leading the field, when you’re at the cutting edge of developments, there’s often not one right way of going forward. You’re ahead now, and you have to decide which path to cut. Should you use IPA or grounded theory? Two or three levels in your multilevel analysis? Well, sorry, but as your supervisors, examiners, and readers it’s very likely that we don’t actually know. We’ve got our own ideas, but what we’re hoping for is that you’ll be able to face those really difficult questions and, in the absent of any certainties, work if out for yourself (in a sensible, informed, and transparent way). And that’s not because we want to provide a non-directive environment to teach you to work these things out for yourself: it’s because we genuinely, really, don’t know.

That’s what doctoral level competences are about: being able to move forward in the face of incomplete knowledge. If you don’t know, it’s almost certainly not because you are incapable or dumb, but because the reality is that no one else knows either: no one has managed to work it out yet. And what we’re hoping for is that you’ll do the work of working it out. There’s so many questions, uncertainties, and unknowns out there; and if you can take one small chunk of this and do some thinking that can contribute to the wider field, you’ll be doing a massive benefit to all of us.

Conclusion

Be serious, then, about your research. You do nothing for yourself, or for the field, if you treat your research as simply an academic exercise that you have to get through—that isn’t ever going to teach anyone about anything. Sorry if that sounds harsh; but be serious about your research in the same way that you would be serious about your work as a therapist. That doesn’t mean not being able to laugh, or joke, or enjoy it along the way; but it does mean having the confidence to believe that you can give something meaningful to the wider world. And if you don’t feel that, take some time to work on it, in the same way that you would work on your insecurities as a therapist (in research supervisor, for instance, or in therapy, or on your course). Get to a position where, in transactional analysis terms, you’re an adult: where you’re able to own your strengths and your abilities to contribute, as well as your limitations. You have so much to offer.

---

Acknowledgements

Photo by Ben White on Unsplash

Disclaimer

 The information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

Research Aims and Questions: Some Pointers

Your aims are the beating heart of your research project, and your write-up. Whether you are conducting an exploratory study or a hypothesis testing one, whether qualitative of quantitative, you are trying to do something in your research, and specifying what that doing is is the key that holds your project together.

Wherever you are in a research project, try specifying exactly what your aims for it are, for instance:

In this project… I am trying to discover how clients’ experience preference work

In this project… I am trying to find out if school counselling is effective

In this project… I am trying to assess the psychometric properties of the Goals Form

In research, the aim is to always find something out, so it’s always possible to also reframe your aims as a question:

How do clients’ experience preference work?

Is school counselling is effective?

What are the psychometric properties of the Goals Form?

Framing it either way is fine. But it’s essential that your aims and your questions match, and it’s generally helpful to be aware of both forms as you progress through your research.

If you’re struggling to articulate the aims of your research, ask a friend or peer to ‘interview’ you about it. They can ask you questions like:

• ‘What are you trying to find out?’

• ‘What’s the question that you are asking?’

• ‘What do you want to know that isn’t known up to this point?’

• ‘What kind of outcome to this project would tell you it’s been a successful one?’

Trying to articulate your research aims/questions isn’t always easy, and it’s generally an iterative process: one that develops as your research progresses. Sometimes, it’s a bit like an ‘unclear felt sense’ (from the world of focusing): you kind of ‘know’ what the aim is, but can’t quite put it into words. It’s on the tip of your tongue. That’s why it can be helpful to have a colleague interview you about it so you can try and get it more clearly stated.

Another way into this would be to ask yourself (or discuss with peers):

• ‘What might be meaningful findings from my project?’

For instance, with the research questions above, meaningful findings might be that ‘clients find it irritating to be asked about their preferences’, or that ‘the Goals Form has good reliability but poor validity?’ Of course, you don’t want to pre-empt your answers, but just seeing if there are potential meaningful answers is a good way of checking whether your question makes sense and is worth asking. If you find, for instance, that you just can’t envisage a meaningful answer, or that the only meaningful answers are ones that you already know about, it may mean that you need to rethink your research question(s). There needs to be, at least potentially, the possibility of something interesting coming out of your study.

You may have just one aim, you may have more than one aims. A few aims is fine, but make sure there aren’t too many, and make sure you’re clear about what they are and how they differ. Disentangling your aims/research questions can be complex, but it’s essential in a research project to be able to do that: so that you and whoever reads your research knows what it’s all about, and what your contribution to knowledge might be.

If you find it difficult to articulate your aim(s), it may be that, at the end of the day, you’re not really sure what your research is about. That’s fine: it’s a place that many of us get to, particularly if our research has gone through various twists and turns. So it’s not something to beat yourself up about, but it is something to reflect on and see if you can re-specify what it is, now, that you’re trying to do and ask, so that you can be clear. This may mean turning away from some of the things you’ve been interested in, or some of the questions that you were originally asking. It can be sad to let go of aims and questions; but it’s generally essential in ensuring you’ve got a nice, clear, focused project—not one where you’re going to be lost in a forest of questions and confusion.

If you specify your aims but can’t rephrase them as questions that’s also worth noting. That may be an indicator that really what you are trying to do is to prove something, rather than conducting a genuine inquiry. For instance, you may find that your aim is, ‘to show that people living in poverty cannot access counselling?’ or ‘to establish that female clients prefer self-disclosure to male clients’. If that’s the case, try and find a way of re-framing your research in terms of an open question(s): one(s) that you genuinely don’t know the answer to. It’s so much more powerful, interesting, and meaningful to conduct research that way. Indeed, if you’re struggling to articulate your research question, one really valuable question to ask yourself is:

• ‘What is the question that I genuinely don’t know the answer to?’

And ‘genuinely’ here does mean genuinely. If you’re pretending to yourself that you don’t know something so that you can show it anyway, then that’s likely to become evident when you write up your research. So really see if you can find a question that you genuinely, really genuinely, can’t answer at this point—but one that you would really love to be able to. That’s a fantastic place to start research from.

Once you’ve got your beating heart, write it up on a stick it note and put it on your wall somewhere or put it on your screensaver. Keep it in mind all the time: the aims of your research and the questions you’re asking. When you’re interviewing your participants, when you’re doing your analysis… keep coming back to it again and again. It’ll keep you focused, it’ll mean that you keep on track, and it’ll keep you with a clear sense of where it is you want to go and what you are trying to do.

If you deviate, that’s fine, we all do that. Just like in meditation, notice you’re moving on, then try and bring yourself back. Or, if you really can’t bring yourself back to your aims/questions, then it may be that they need to change. That’s fine in a research project and it does happen but, again, be clear and specific about what the aims and questions are changing to, and make sure that the rest of your project is then aligned with those new directions. What you don’t want, for instance, is a Literature Review asking one set of questions, and then a Results section that answers an entirely (or even slightly) different set of aims.

And when you write up your thesis or research paper, start with your aim(s)/question(s). Often people put them towards the end of the Literature Review (i.e., just before the Methods section), but you can also put them earlier on in your Introduction. Write them down just as they have been formulated as you’ve progressed: clear, succinct, a line or two for each. If there’s more than one, write them down clearly as separate aims/questions. You probably don’t need to give them in both formats and you could use different formats in different places: for instance, they could be stated as aims in your Abstract and Introduction, then as questions just before your Methods section.

Once you’ve got those aims/questions stated, you can build all the other parts of the research and write-up around it. For instance:

• Literature Review section: You can structure this by the questions you’re asking, with different sections looking at what we know, so far, in relation to each question.

• Interview questions: In most instances, the questions you ask your participants should match, pretty much exactly, your overarching research questions. So if you are interested in how clients experience preference work… ask them. No need to faff about with indirect or tangential interview questions: just go into the heart of what you really want to know, and have a rich, complex, multifaceted dialogue about it.

• Results section: Whether qualitative or quantitative, you can present your findings by research question: So what did you find in relation to question a, then in relation to question b, etc.

• Discussion section: This, too, can be structured by research question—though I would tend to do this in the Discussion or in the Results (not both), so that the sections don’t overlap too much with each other.

• Limitations: Don’t just say what’s good or bad about your research: say how the answer you got to your questions might have been biased by particular factors, and what that might mean.

• Abstract: When you come on to write this, make sure your aims/questions are clearly stated, and then clear answers to each question are given.

Being clear about your research aims and questions, and focusing your research around them, may seem obvious. It may also seem pedantic or overly-explicit. But it’s key to creating a coherent, focused research project that—as required at master’s or doctoral level—makes a contribution to knowledge. It can be hard to do; but working out, for yourself, what you are trying to do and ask is a key element of the research process. Research isn’t just a question of mucking in, generating data, and leaving it to your reader (or your assessor) to work out what it all means. You need to do that: to guide the reader from question(s) to answer(s), and to help them see how the world is a better-understood place (even if it’s just a little better understood) for what you have done.

Acknowledgements

Photo by Bart LaRue on Unsplash

DISCLAIMER

The information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

The Introduction: Some Pointers

The following blog is for Master’s or doctoral level students writing research dissertations in the psychological therapies fields. The pointers are only recommendations—different trainers, supervisors, and examiners may see things very differently.

What does an Introduction do?

The aim of an introductory section is to help your reader understand what your dissertation is about and why it is important. It is also an opportunity to help them understand the context for your study so that they can understand where it is coming from and what it is trying to contribute to the wider field. 

An Introduction will typically include the following sections, though not necessarily in this order:

• Aims/objectives of the research

• Research question(s)

• Personal rationale

• Contextual rationale

• Background literature

• Definitions of key terms

• Outline of the dissertation

For a dissertation, an Introduction is often separate from a Literature Review. The former is often the place where you set out why you are asking this question(s), whereas the latter sets out what you already know in answer to this question(s).

Aims/Questions

What is the purpose of your research? Your Introduction is the place to try and state, as explicitly as possible, what your research aims and/or questions are (see pointers here).

Personal Rationale

So why are you doing it? Why is it important to you? In most therapeutic fields, it is entirely legitimate (if not essential) to say something of why you are coming to this question, at this point in time. And the deeper you can go into your own personal rationale, the more insightful and authentic your personal account is likely to be. So some questions you might want to ask yourself are:

• Why this research question/topic area?

• Why does it matter to you?

• What does it mean to you?

• Why now?

• What was your personal journey towards this research question?

• How do you feel about this research question? What emotions are generated in you when you think about it?

• How does this research question connect to your:

  • life

  • personal history

  • identity

  • values and meanings

  • aspirations for the future?

Something you might find really helpful is to do this as an exercise with a partner. Ask them to interview you, say for 20 minutes, using these questions. Record it and then listen back once the interview is over. That can really free you up to talk honestly and openly about some of the concerns and motives that underpin why you are doing this work. And, of course, you don’t need to share it all in your Introduction: but knowing where you want to go and why is a critical part of conducting an informed, in-depth, and self-reflexive study.

As part of this reflexive work, you might also want to ask yourself the question, ‘Are there some particular answers that I, consciously or unconsciously, would “like” to find?’ When it comes to writing about your personal biases in relation to the research question, however, that may be more likely to go in your Methods section. Here, in the Introduction, the focus is more on biases and assumptions that may have led you to ask this question in the first places.

Contextual Rationale

Of course, it’s not all about you. There’s also got to be good reasons, for the wider field, in you asking these questions at this point in time. For instance, maybe there’s a lot of research on how young people experience acceptance and congruence, but not empathy; or perhaps there’s evidence of particular increases in mental health problems in young people of Asian origin, so we really need to know what can help them.

So your Introduction is also a place where you can say about why your research is of importance in the grander scheme of things. Use evidence wherever you can, though it might be historical or socio-political as well as psychological.

Again, it can be really helpful to explore these questions in a pair. Get interviewed by a colleague, but this time invite them to probe you on why they should care about what you are doing. Some questions that they might want to ask/role-play are:

• Why should I (as a counsellor/psychotherapist/counselling psychologist/researcher/commissioner/policy-maker) care about what you are doing?

• What is it going to teach me, as a counsellor/psychotherapist/counselling psychologist/researcher/commissioner/policy-maker?

• Don’t people already know the answer to your question? How is it going to add to the literature out there?

• Why is it worth anyone spending time on this?

• How will it make a contribution to:

  • Society?

  • Clients?

  • Other therapists?

  • The people who took part in the study?

Have you convinced them it is worthwhile (indeed, have you convinced yourself)? If not, it may be worth spending some time thinking through what it is that you really want to do, and whether it really is important. It may be that you sense it, it’s just difficult putting it into words. But try and find that sense so that you have a really clear basis to underpin your research work.

Background literature

Your Introduction is also a good place to explain anything that the reader needs to know about to understand the context and meaning of your study. For instance, how many young people enter person-centred therapy every year, or how did the concept of ‘alliance ruptures’ emerge and what are it’s theoretical underpinnings.

Of course, you’re also going to be reviewing the background literature in your Literature Review chapter, so how do you know what goes where? Maybe the best way to think about this, as above, is that content for the Literature Review chapter provides preliminary answers to your questions, whereas content for the Introductory chapter helps you understand what the question is and why it’s important. So, for instance, in our study of young people’s experiences of empathy, literature on how Rogers defined empathy might go in our Introduction, as might literature on mental health problems in adolescents. But findings of, for instance, a quantitative study on how young people rated the importance of empathy would go in our Literature Review, because it’s providing us with some important initial answers to the question we are asking.

Defining Key Terms

Closely related to this, what we can also do in our Introduction is to define key terms: anything that the reader is going to need to understand to be able to make sense of our thesis; and also so that they know how we, specifically, are choosing to use certain terms. For instance, do we mean ‘empathy’ as Rogers defined it, or as neuroscientists have understood it, or in the Kohutian sense? That’s very important information for the reader in terms of understanding our work.

What about if we want to leave the definition(s) open to our participants rather than imposing on them a particular understanding? Indeed, maybe our research is about exploring what young people understand by empathy, or what alliance ruptures mean to clients.

Research questions of this type (‘What do people understand by x?’) can be great, particularly if we’re coming to our research from a very inductive, ‘grounded’ epistemological position. However, I would say that it is a case of either/or: that is, either ask about what something means, or ask about how it is experienced/what it does—but don’t try asking both of these questions at the same time. Otherwise, you’re essentially asking your participants to describe the experience/effects of lots of different things, and you’re not likely to come up with a particular coherent answer. If Person A, for instance, defines empathy as Z, and experiences it as V; and Person B defines empathy as Y, and experiences it as U; then we may have learnt about different definitions of empathy, but our findings of V and U don’t really mean much because they refer to different things (Z and Y).

Outline Structure

Finally, your Introduction is a place where you can say what your thesis is going to look like: leading the reader through the different chapters of your work so that they know what is to come. You don’t need to do too much detail, maybe just a page or so, but something that gives them a clear and coherent sense of the route ahead.

Conclusion

By the end of your Introduction, your reader should have all they need to embark on the journey of your thesis; and, ideally, be motivated and excited to travel forward. So do make sure, as you describe your reasons for doing this work, or what the work is about, that you also draw the reader in: interest them, compel them, make them want to know more. Think of it like a tourist guide preparing your traveller for a trip ahead. Tell them what they need to know, but also not everything. After all, you want them to experience it first hand, and to learn what you have learnt as you travelled into the heart of your research.

DISCLAIMER

The information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

Evaluating and Auditing Counselling and Psychotherapy Services: Some Pointers

How do you go about setting up an evaluation or audit of your therapy service—whether it’s a large volunteer organisation or your own private practice?

Clarifying your Aims

There’s lots of reasons for setting up a service evaluation or audit, and being clear about what your’s are is a vital first step forward. Some possible aims might be:

• Showing the external world (e.g., commissioners, policy makers, potential clients) that your therapy is effective.

• Knowing for yourself, at the practitioner or service level, what’s working well and what isn’t.

• Enhancing outcomes by providing therapists, and clients, with ‘systematic feedback’.

• Developing evidence for particular forms of therapy (e.g., person-centred therapy) or therapeutic processes (e.g., the alliance).

And, of course, there’s also:

• Because you have to!

Choosing an Evaluation Design

There’s lots of different designs you can adopt for your evaluation and audit study, and these can be combined in a range of ways.

Audit only

This is the most basic type of design, where you’re just focusing on who’s coming in to use your service and the type of service you are providing.

Pre-/Post-

This is probably the most common type of evaluation design, particularly if your main concern is to show outcomes. Here, clients’ levels of psychological problems are assessed at the beginning and end of therapy, so that you can assess the amount of change associated with what you’re doing.

Qualitative

You could also choose to do interviews with clients at the end of therapy about how they experienced the service. A simpler form of this would be to use a questionnaire at the end of treatment. John McLeod has produced a very useful review of qualitative tools for evaluation and routine outcome monitoring (see here).

Experimental

If you’ve got a lot of time and resources to hand—and/or if you need to provide the very highest level of evidence for your therapy—you could also choose to adopt an experimental design. Here, you’re comparing changes in people who have your therapy with those who don’t (a ‘control group’). These kinds of studies are much, much more complex and expensive than the other types, but they are the only one that can really show that the therapy, itself, is causing the changes you’ve identified (pre-/post- evaluations can only ever show that your therapy is associated with change).

Choosing Instruments

There’s thousands of tools and measures out there that can be used for evaluation purposes, so where do you start?

Tools for use in counselling and psychotherapy evaluation and audit studies can be divided into three types. These are described below and, for each type, I have suggested some tools for a ‘typical’ service evaluation in the UK. Unless otherwise stated, all these measures are free to use, well-validated (which means that they show what they’re meant to show), and fairly well-respected by people in the field. All the measures described below are also ‘self-rated’. This means that clients, themselves, fill them in. There are also many therapist- and observer-rated measures out there, but the trend is towards using self-rated measures and trusting that clients, themselves, know their own states of mind best.

Just to add: however tempting it might be, I’d almost always you not to develop your own instruments and measures. You’d be amazed how long it takes to create a validated measure (we once took about six years to develop one with six items!) and, if you create your own, you can never compare your findings with those of other services. Also, for the same reason, it is almost always unhelpful to modify measures that are out in the public domain—even minimally. Just changing the wording on an item from ‘often’ to ‘frequently’, for instance, may make a large difference in how people respond to it.

Outcome Tools

Outcome tools are instruments that can be used to assess how well clients are getting on in their lives, in terms of symptoms, problems, and/or wellbeing. These are the kinds of tools that can then be used in pre-/post-, or experimental, designs to see how clients change over the course of therapy. These tools primarily consist of forms with around 10 ‘items’ or so, like, ‘I’ve been worrying’ or ‘'I’ve been finding it hard to sleep’. The client indicates how frequently or how much they have been experiencing this, and then their responses can be totalled up to give an overall indication of their mental and emotional state.

Its generally good practice to integrate clients’ responses to the outcome tools into the session, rather than divorcing them from the therapeutic process. For instance, a therapist might say, ‘I can see on the form that this has been a difficult week for you,’ or, ‘Your levels of anxiety seem to be going down again.’ This is particularly important if the aim of the evaluation is to enhance outcomes through systematic feedback.

General

A popular measure of general psychological distress (both with therapists and clients), particularly in the UK, is:

• CORE-OM

This can be used in a wide range of services to look at how overall levels of distress, wellbeing, and functioning change over time. A shortened, and more easily usable version of this (particularly for weekly outcome monitoring, see below), is:

• CORE-10

Another very popular, and particularly brief, general measure of how clients are doing is:

• Outcome Rating Scale (available via license)

Two other very widely used measures of distress in the UK are:

• PHQ-9

• GAD-7

The PHQ-9 is a depression-specific measure, and the GAD-7 is a generalised-anxiety specific measure, but because these problems are so common they are often used as general measures for assessing how clients are doing, irrespective of their specific diagnosis. They do also have the dual function of being able to show whether or not clients are in the ‘clinical range’ for these problems, and at what level of severity.

Problem-specific

There are also many measures that are specific to particular problems. For instance, for clients who have experienced trauma there is:

• Impact of Events Scale (revised)

And for eating problems there is:

• Eating Attitudes Test

If you are working in a clinic with a particular population, it may well be appropriate to use both a general measure, and one that is more specific to that client group.

Wellbeing

For those of us from a more humanistic, or positive psychology, background, there may be a desire to assess ‘wellness’ and positive functioning instead of (or as well as) distress. Aside from the ORS, probably the most commonly used wellbeing measure is:

• WEMWBS

• Authenticity Scale

There’s both a 14-item version, and shortened 7-item version for more regular measurement.

Personalised measures

All the measures above are nomothetic, meaning that they have the same items for each individual. This is very helpful if you want to compare outcomes across individuals, or across services, and to use standardised benchmarks. However, some people feel that it is more appropriate to use measures that are tailored to the specific individual, with items that reflect their unique goals or problems. In the UK, probably the best known measure here is:

• PSYCHLOPS

This can be used with children and young people as well as adults, and invites them to state their specific problem(s) and how intense they are. Another personalised, problem-based tool is:

• Personal Questionnaire

If you are more interested in focusing on clients’ goals, rather than their problems, then you can use:

• Goals Form

Service Satisfaction

At the end of therapy, clients can be asked about how satisfied they were with the service. There isn’t any one generic standard measure here, but the one that seems to be used throughout IAPT is:

• Patient Experience Questionnaire

Children and young people

The range of measures for young people is almost as good as it is for adults, although once you get below 11 years old or so the tools are primarily parent/carer- or teacher-report. Some of the most commonly used ones are:

• YP-CORE: Generic, brief distress outcome measure

• SDQ: Generic distress outcome measure, very well validated and in lots of languages

• CORS: Generic, ultra-brief measure of wellbeing (available via license)

• RCADS: Diagnosis-based outcome measure

• GBO Tool: Personalised goal-based outcome measure

• ESQ: Service satisfaction measure.

A brilliant resource for all things related to evaluating therapy with children and young people is corc.uk.net/

Process Tools

Process measures are tools that can help assess how clients are experiencing the therapeutic work, itself: so whether they like/don’t like it, how they feel about their therapist, and what they might want differently in the therapeutic work. These are less widely used than outcome measures, and are more suited to evaluations where the focus is on improving outcomes through systematic feedback, rather than on demonstrating what the outcomes are.

Probably the most widely used process measure in everyday counselling and psychotherapy is:

• SRS (available via license)

This form, the Session Rating Scale, is part of the PCOMS family of measures (along with the ORS), and is an ultrabrief tool that clients can complete at the end of each session to rate such in-session experiences as whether they feel heard and understood.

For a more in-depth assessment of particular sessions, there is:

• Helpful Aspects of Therapy Form

This has been widely used in a research context, and includes qualitative (word-based) as well as quantitative (number-based) items.

Several well-validated research measures also exist to assess various elements of the therapeutic relationship. These aren’t so widely used in everyday service evaluations, but may be helpful if there is a research component to the evaluation, or if there is an interest in a particular therapeutic process. The most common of these is:

• Working Alliance Inventory

This comes in various version, and assesses the clients’ (or therapists’) view of the level of collaboration between members of the therapeutic dyad. Another relational measure, specific to the amount of relational depth, is:

• Relational Depth Frequency Scale

A process tool that we have been developing to help elicit, and stimulate dialogue on, clients’ preferences for therapy is:

• Cooper-Norcross Inventory of Preferences

This invites clients to indicate how they would like therapy to be on a range of dimensions, such that the practitioner can identify any strong preferences that the client has. This can either be used at assessment, or in the ongoing therapeutic work. An online tool for this measure can be accessed here.

Interviews

If you really want to find out how clients have experienced your service, there’s nothing better you can do than actually talk to them. Of course, you shouldn’t interview your own clients (there would be far too much pressure on them to present a positive appraisal) but an independent colleague or researcher can ask some key questions (for instance, ‘What did you find helpful? What did you find unhelpful? What would you have liked more/less of?) which can be shared with the therapist or the service more widely (with the client’s permission). There’s also an excellent, standardised protocol that can be used for this purposes:

• Change Interview

Note, as an interviewing approach has the potential to feel quite invasive to clients (though also, potentially, very rewarding), it’s important to have appropriate ethical scrutiny here of procedures before carrying these out.

Children and young people

Process tools for children and young people are even more infrequent, but there is the child version of the Session Rating Scale:

• CSRS

Demographic/Service Audit Tools

As well as knowing how well clients are doing, in and out of therapy, it can also be important to know who they are—particularly for auditing purposes. Demographic forms gather data about basic characteristics, such as age and gender, and also the kinds of problems or complexity factors that clients are presenting with. These tools do tend to be less standardised than outcome or process measures, and it’s not so problematic here to develop your own forms.

For adults, a good basic assessment form is:

• CORE Assessment Form

For children and young people, one of the most common, and thorough, forms is:

• Current View

Choosing Measurement Points

So when are you actually going to ask clients, and/or therapist, to complete these measures? The demographic/audit measures can generally be done just once at the beginning of therapy, although you may want to update them as you go along. Service satisfaction measures and interviews tend to be done just at the end of the treatment.

For the other outcome and process measures, the current trend is to do them every session. Yup, every session. Therapists often worry about that—indeed, they often worry about using measures altogether—but generally the research shows that clients are OK with it, provided that they don’t take up too much of the session (say not more than 5-10 minutes in total). So, for session-by-session outcome monitoring, make sure you use just one or two of the briefer forms, like the CORE-10 or SRS, rather than longer and more complex measures.

Why every session? The reason is that clients, unfortunately, do sometimes drop out, and if you try and do measures just at the beginning and end you miss out on those clients who have terminated therapy prior to a planned ending. In fact, that can give you better results (because you’re only looking at the outcomes of those who finished properly, who tend to do better) but it’s biased and inaccurate. Session by session monitoring means that you’ve always got a last score for every client, and now most funders or commissioners would expect to see data gathered in that way. If you’ve only got results from 30% of your sample, it really can’t tell you much about the overall picture.

Generally, outcome measures are completed at the start of a session—or before the start of a session—so that clients’ responses are not too affected by the session content. Process measures are generally completed towards the end of a session as they are a reflection on the session itself (but with a bit of time to discuss any issues that might come up).

Analysing the Data

Before you start a service evaluation, you have to know what you are going to do with the data. After all, what you don’t want is to a big pile of CORE-OM forms in one corner of your storage room!

That means making sure you price in to any evaluation the costs, or resources, of inputting the data, analysing it, and writing it up. It simply not fair to ask clients, and therapists, to use hundreds of evaluation forms if nothing is ever going to happen to them.

The good news is that most of the forms, or the sites that the forms come from, tell you how to analyse the data from that form.

The simplest form of analysis, for pre-/post- evaluations, is to look at the average score of clients at the beginning of therapy on the measure, and then their average score at the end. Remember to only use clients who have completed both pre- and post- forms. That will show you whether clients are improving (hopefully) or getting worse.

With a bit more sophisticated statistics you can calculate what the ‘effect size’ is. This is a standardised measure of the magnitude of change (after all, different measures will change by different amounts). The effect size can be understood as the difference between pre- and post- scores divided by the ‘standard deviation’ of the pre- scores (this is the amount of variation in scores, which you can work out via Excel using the function ‘stdev’). Typically in counselling and psychotherapy services, the effect size is around 1, and you can compare your statistics with other services in your field, or with IAPT, to see how your service is doing (although, of course, any such comparisons are ultimately very approximate).

What you can also do is to find out the percentage of your clients that have shown ‘reliable change’ (which is change more than a particular amount, to compensate for the fact that measures will always be imprecise), and ‘clinical change’ (the amount of clients who have gone from clinical to non-clinical bands and vice versa). If you look around on the internet, you can normally find the clinical and reliable change ‘indexes’ for the measures that you are using (though some don’t have them). For the PHQ-9 and GAD-7, you can look here to see both calculations for reliable and clinical change, and the percentages for each of these statistics that were found in IAPT.

Online Services

One way around having to input and analyse masses of data yourselves is to use an online evaluation service. This can simplify the process massively, and is particularly appropriate if you want to combine service evaluation with regular systematic feedback for clinicians and clients. Most of these (though not all) can host a wide range of measures, so they can support the particular evaluation that you choose to develop. However, these services come at a price: a license, even for an individual practitioner, can be in the hundreds or thousands of pounds. Normally, you’d also need to cost in the price of digital tablets for clients to enter the data on.

My personal recommendation for one of these services is:

• Pragmatic Tracker

At the CREST Research Clinic we’ve been using this system for a few years now, and we’ve been consistently impressed with the support and help we’ve received from the site developers. Bill and Tony are themselves psychotherapists with an interest in—and understanding of—how to deliver the best therapy.

Other sites that I would recommend for consideration, but that I haven’t personally used, are:

• Core Systems Trust: Particularly if you’re using the CORE family of tools, but they support other ones too.

• Better Outcomes Now: for accessing the PCOMS tools (but not other measures). Also see My Outcomes for these measures.

• OQ Measures: A US company, based around the Outcome Questionnaire.

Challenges

In terms of setting up and running a service evaluation, one of the biggest challenges is getting counsellors and psychotherapists ‘on board’. Therapists are often sceptical about evaluation, and feel that using measures goes against their basic values and ways of doing therapy. Here, it can be helpful for them to hear that clients, in fact, often find evaluation tools quite useful, and are often (though not always) much more positive about it than therapists may assume. It’s perhaps also important for therapists to see the value that these evaluations can have in securing future funding and support for services.

Another challenge, as suggested above, is simply finding the time and person-power to analyse the forms. So, just to repeat, do plan and cost that in at the beginning. And if it doesn’t feel like that is going to be possible, do consider using an online service that can process the data for you.

For the evaluation to be meaningful, it needs to be consistent and it needs to be comprehensive. That means it’s not enough to have a few forms from a few clients across a few sessions, or just forms from assessment but none at endpoint. Rather, whatever you choose to do, all therapists need to do it, all of the time. In that respect, it’s better just to do a few things well, rather than trying to overstretch yourself and ending up with a range of methods done patchily.

Some ‘Template’ Evaluations

Finally, I wanted to suggest some examples of what an evaluation design might look like for particular aims, populations, and budgets:

Aim: Showing evidence of effectiveness to the external world. Population: adults with range of difficulties. Budget: minimal

• CORE-10: Assessment, and every session

• CORE Assessment Form

• Analysis: Service usage statistics; pre- to post- change, effect size, % reliable and clinical change

Aim: Showing evidence of effectiveness to the external world, enhancing outcomes. Population: young people with range of difficulties. Budget: minimal

• YP-CORE: Assessment, and every session

• Current View: Assessment

• ESQ: End of therapy

• Analysis: Service usage statistics; pre- to post- change, effect size, % reliable and clinical change; satisfaction (quantitative and qualitative analysis)

Aims: Showing evidence of effectiveness to the external world, enhancing outcomes. Population: adults with depression. Budget: medium

• PHQ-9: Assessment and every session

• CORE Assessment Form

• Helpful Aspects of Therapy Questionnaire

• Patient Experience Questionnaire: End of Therapy

• Analysis: Service usage statistics; pre- to post- change, effect size, % reliable and clinical change; helpful and unhelpful aspects of therapy (qualitative analysis); satisfaction (quantitative and qualitative analysis)

And finally…

Please note, the information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website or any external internet sites referenced in or linked in this blog. I also can’t offer advice on individual evaluations. Sorry… but hope the information here is useful.

Publishing your research: Some pointers

Why bother?

Let’s say this, up front: it’s hard work getting your research published. It’s rarely just a case of cutting and pasting a few bits of your thesis, or reformatting an SPSS table or two, and then sending it off to the BMJ for their feature article. So before you do anything, you really need to think, ‘Have I got the energy to do it?’ ‘Do I really want to see this in print?’ And being clear about your reasons may give you the motivation to keep going when every part of you would rather give up. So here’s five reasons why you might want to publish your research.

1.  If you want to get into academia, it’s pretty much essential. It’s often, now, the first thing that an appointment panel will look at: how many publications you have, and in what journals. 

2. Even if your focus is primarily on practice, a publication can be great in terms of supporting your career development. It can look very impressive on your CV—particularly if it’s in an area you’re wanting to develop specialist expertise in. Indeed, having that publication out there establishes you as a specialist in that field, and that can be great in terms of being invited to do trainings, or teaching on courses, or consultancy.

3. It’s a way of making a contribution to your field—and that’s the very definition of doctoral level work. You’ve done your research, you’ve found out something important, so let people know about it. If you’ve written a thesis, it may just about be accessible to people somewhere in your university library, but they’re going to have to look pretty hard. If it’s in a journal, online, you’re speaking to the world.

4. …And that means you’re part of the professional dialogue. It’s not just you, sitting in your room, talking to your cat: you’re exchanging ideas and evidence with the best in the field—learning, as well as being learnt from.

5. You owe it to your participants. For me, that’s the most important reason of all. Your participants gave you their time, they shared with you their experiences—sometimes very deeply.  So what are you going to do with that? Are you just going to use it to get your award—for your own private knowledge and development; or are you going to use it to help improve the lives of the people that your participants represent? In this sense, publishing your work can be seen as an ethical responsibility.  

Is IT good enough?

Yes. Almost certainly. If it’s been passed, at Master’s level and especially at doctoral, it means, by definition, that it’s at a good enough standard for publication somewhere. It’s totally understandable to feel insecure or uncertain about your work—we all can have those feelings—but the ‘objective’ reality is that it’s almost certainly got something of originality, significance, and rigour to contribute to the public domain.

Focus

If you’ve written a thesis—and particularly a doctoral one—you may have been covering several different research questions. So being clear about what you want to focus on in your publication, or publications, may be an important next step. Get clear question(s), and be clear about the particular methods and parts of your thesis that answer them. That means that some of your thesis has to go. Yup, that’s right: some of that hard fought, painful, agonised-over-every-word-at-four-in-the-morning will have to be the mercy of your Delete key. That can be one of the hardest parts of converting your thesis to a publication—it’s a grieving process—but it’s essential to having something in digestible form for the outside world.

And, of course, you may want to try and do more than one publication. For instance, you might report half of your themes in one paper, and then the other half in another paper; or, if you did a mixed methods study, you could split it into quant. and qual. Or you might divide your literature review off into a separate paper, or do a focused paper on your methodology. ‘Salami slicing’ your thesis too much can end up leaving each bit just too thin, but if there’s two or more meaningful chunks that can come of your work, why not? 

Finding the right journal

This is one of the most important parts of writing up for publication, and easily overlooked. Novice researchers tend to think that, first, you do all your research, write it up for publication, and then only at the end do you think about who’s going to publish it. But different journals have different requirements, different audiences, and publish different kinds of research; so it’s really important to have some sense of where you might submit it to long before you get to finishing off your paper. That means you should have a look at different journal website, and see what kinds of papers they publish and who they’re targeted towards—and take that into account when you draft your article. 

Importantly, each journal site will have ‘Author Guidelines’ (see, for instance, here) and these are essential to consult before you submit to that journal. To be clear, these aren’t a loose set of recommendations for how they’d like you to prepare your manuscript. They’re generally a very strict and precise set of instructions for the ways that they want you to set it out (for instance, line spacing, length of abstract), and if you don’t follow them, you’re likely to just get your manuscript returned with an irritated note from the publishing team. Particularly important here is the length of article they’ll accept. This really varies across journals, and is sometimes by number of pages (typically 35 pages in the US journals), sometimes by number of words (generally around 5-6,000 words)—and may be inclusive of references and tables, etc., or not. So that’s really important to find out before you submit anywhere, as you may find out that you’re thousands of words over the journal’s particularly limit. Bear in mind that, particularly with the higher impact journals (see below), they’re often looking for reasons to reject papers. They’re inundated: rejecting, maybe, 80% of the papers submitted to them. So if they don’t think you’ve bothered to even look at their author guidelines, they may be pretty swift in rejecting your work.  

So which journals should you consider? There’s hundreds out there and it can feel pretty overwhelming knowing where to start. One of the first choices is whether to go with a general psychotherapy and counselling research journal, or whether something more specific to the field you’re looking at. For instance, if your research was on the experiences of clients with eating disorders in CBT, you could go for a specialised eating disorders journal, or a specialised CBT journal, or a more general counselling/psychotherapy publication. This can be a hard call, and generally you’re best off looking at the journal sites, as above, to see what kind of articles they carry and whether your research would fit in. 

Note, a lot of psychotherapy and mental health journals don’t publish qualitative research, or only the most positivist manifestations of it (i.e., large Ns, rigorous auditing procedures, etc.). It’s unfortunate, but if you look at a journal’s past issues (on their site) and don’t see a single qualitative paper, you may be wasting your time with a qualitative submission: particularly if it’s underlying epistemology is right at the constructionist end of the spectrum. And, if you’re aiming to get your qualitative research published in one of the bigger journals, it’s something you may want to factor in right at the start of your project: for instance, with a larger number of participants, or more rigorous procedures for auditing your analysis.

You should also ask your supervisor, if you have one, or other experienced people in the field, where they think you should consider submitting to. If they’ve worked in that area for some time, they should have some good ideas.  

Impact factor

Another important consideration is the journal’s impact factor. This is a number from zero upwards indicating, essentially, how prestigious the journal is. There’s an ‘official’ one from the organisation Clarivate; but these days most journals will provide their own, self-calculated impact factor if they do not have an official one. You can normally find the impact factor displayed on the journal’s website (the key one is the ‘two year’ impact factor—sometimes just called the ‘impact factor’—as against the five year impact factor). To be technical, the impact factor is the amount of times that the average article in that journal is cited by other articles over a particular period: normally two years. So the bigger the journal’s impact factor, the more that articles in that journal are getting referenced in the wider academic field—i.e., impact. The biggest international journals in the psychotherapy and counselling field will have an impact factor of 4 or 5, and ones of 2 or 3 are still strong international publications. Journals with an impact factor around 1 may tend towards a national rather than international reach, and/or be at lower levels of prestige, but still carrying many valuable articles. And some good journals may not have an official impact factor at all: journals have to apply for an official one and in some cases the allocation process can seem somewhat arbitrary.

Of course, the higher the journal’s impact factor, the harder it is to get published there, because there’s more people wanting to get in. So if you’re new to the research field, it’s a great thing to get published in a journal with any impact factor at all; and you shouldn’t worry about avoiding a journal just because it doesn’t have an impact factor, or if it’s fairly low. At the same time, if you can get into a journal with an impact factor of 1 or above that’s a great achievement, and something that’s likely to make your supervisor(s), if they’re co-authors on the paper (see below), very happy. For more specific pointers on publishing in higher impact journals, see here.

These days, the impact of a journal may also be reported in terms of its quartile: so from Q1 to Q4.  Essentially Q1 journals are those with impact factors within the top 25% of the subject area, and down to Q4 journals which are in the lowest 25%.  

In thinking about impact factor, a key question to ask yourself is also this: Do I want to (a) just get something out there with the minimum of additional effort, or (b) try and get something into the best possible journal, even if it takes a fair bit of extra work. There’s no right answers here: if you have got the time, it’s great if you can commit to (b), but if that’s not realistic and/or you’re just sick and tired of your thesis, then going for (a) is far better than not getting anything out at all.

General counselling and psychotherapy research journals

If you’re thinking of publishing in a general therapy research journal, one of the most accessible to get published in is Counselling Psychology Review – particularly if your work is specific to counselling psychology.  The word limit is pretty restrictive though. There’s also the European Journal for Qualitative Research in Psychotherapy, which is specifically tailored for the publication of doctoral or Master’s research, and aims to ‘provide an accessible forum for research that advances the theory and practice of psychotherapy and supports practitioner-orientated research’. If you’re coming from a more constructionist perspective, a journal like the European Journal of Psychotherapy & Counselling might also be a good first step, which publishes a wide range of papers and perspectives.

For UK based researchers, two journals that are also pretty accessible are Counselling and Psychotherapy Research (CPR) and the British Journal of Guidance and Counselling (BJGC). Both are very open to qualitative, as well as quantitative studies; and value constructionist starting points as well as more positivist ones. The editors there are also supportive of new writers, and know the British counselling and psychotherapy field very well. See here for an example of a recent doctoral research project published in the BJGC (Helpful aspects of counselling for young people who have experienced bullying: a thematic analysis), and here for one in CPR (Helpful and unhelpful elements of synchronous text‐based therapy: A thematic analysis).

 Another good choice, though a step up in terms of getting accepted, is Counselling Psychology Quarterly. It doesn’t have an official impact factor, but it has a very rigorous review process and publishes some excellent articles: again, both qualitative and quantitative.

Then there’s the more challenging international journals, like Journal of Clinical Psychology, Psychotherapy Research, Psychotherapy, and Journal of Counseling Psychology, with impact factors around 3 to 5 (in approximate ascending order). They’re all US-based psychotherapy journals, fairly quantitative and positivist in mindset (though they do publish qualitative research at times), and if you can get your research published in there you’re doing fantastically. Like a lot of the journals in the field, they’re religiously APA in their formatting requirements, so make sure you stick tightly to the guidelines set out in the APA 7th Publication Manual. A UK-based equivalent of these journals, and open-ish to qualitative research (albeit within a fairly positivist frame), is Psychology and Psychotherapy, published by the BPS.

There’s even more difficult ones, like the Journal of Consulting and Clinical Psychology with an impact factor of 4.5, and The Lancet is currently at 53.254.  But the bottom line, particularly if you’re a new researcher, is to be realistic. Having said that, there’s no harm starting with some of the tougher journals, and seeing what they say. At worse, they’re going to reject your paper; and if you can get to the reviewing stage (see below), then you’ll have a really helpful set of comments on how to improve your work. 

If a journal requires you to pay to publish your article, it’s possible a predatory publisher (‘counterfeit scholarly publishers that aim to trick honest researchers into thinking they are legitimate’, see APA advice here). In particular, watch out for emails, once you’ve completed your thesis, telling you how wonderful your work is and how much they want to publish it in their journal—only to find out later that they charge a fortune for it. You may also find yourself getting predatory requests to present your research at conferences, with the same underlying intent. Having said that, an increasing range of reputable journals—particularly online ones that publish papers very quickly, like Trials—do ask authors to pay Article Processing Charges (APC). Generally, you can tell the ‘kosher’ ones by their impact factor and whether they have a well-established international publisher. It’s also very rare for non-predatory journals to reach out to solicit publications. Check with a research supervisor if you’re not sure, but be very, very wary of handing over any money for publication.  

Writing your paper

So you know what you’re writing and who for, now you just have to write it. But how do you take, for instance, your beautiful 30,000 word thesis and squash it down to a paltry 6,000 words?

If you’re trying to go from thesis to article, the first thing is that, as above, you can’t just cut and paste it together. You need to craft it: compiling an integrated research report that is carefully knitted together into a coherent whole. It’s an obvious thing to say, but the journal editors and reviewers won’t have seen your thesis, and they’ll care even less what’s in it. So what they’ll want is a self-contained research report that stands up in its own right—not referring back to, or in the context of, something they’ll never have time to read. That’s particularly important to bear in mind if you’re writing two or more papers from your research: each needs to be written up as a self-contained study, with its own aims, methods, findings, and discussion.

In writing your paper, try and precis the most important parts of your thesis in relation to the question(s) that you’re asking. Take the essence of what you want to say and try and convey it as succinctly and powerfully as possible. Think ‘contracting’ or ‘distilling’: reducing a grape down to a raisin, or a barley mash down to a whiskey—where you’re making it more condensed but retaining all the goodness, sweetness, and flavour. That doesn’t mean you can’t cut and paste some parts of your thesis into the paper, but really ask yourself whether they can be condensed down (for instance, do you really need such long quotes in your Results section?), and make sure you write and rewrite the paper until it seamlessly joins together.

Your Results are generally the most important and interesting part of your paper, so often the part you’ll want to keep as close to its original form as possible. So if you’ve got, say, 7,000 words for your paper, you may want your Results to be 2-3,000 of that (particularly if it’s qualitative). Then you can condense everything else down around it. Your Introduction/Literature Review may be reducible to, perhaps, 500-1,000 words. Maybe 1,000 words for your Methods and Discussion sections; 1,000 words for References. 

If you’ve written a thesis, you may be able to cut some sections entirely. If you’re submitting to a more positivist journal, your reflexivity section can often just go; equally your epistemology. Sorry.  If your study is qualitative, you may also find that you can cut down a lot of the longer quotes in your Results. Again, try and draw out the essence of what you are trying to say there… and just say it.

Generally, and particularly for the higher-end US journals, you’re best off following the structure of a typical research paper (and often they require this): Background, Method, Results, Discussion, References. They’re may be more latitude with the more constructionist journals but, again, check previous papers to see how research has been written up. 

Make sure you write a very strong Abstract (and in the required format for the journal). It’s the first thing that the editor, and reviewers, will look at; and if it doesn’t grab their attention and interest then they may disengage with the rest. There’s some great advice on writing abstracts in the APA 7th Publication Manual as well as on the internet (for instance, here).  

Supervisors and consultants

If you’ve had a supervisor, or supervisors, for your research work, there’s a question of how much you involve them in your publication, and whether you include them as co-author(s). At many institutions, there’s an expectation that, as the supervisor(s) have given intellectual input into the research, they should be included as co-author(s), though normally only as second or third in the list. An exception to the latter might be if a student feels like they don’t want to do any more work at all after they’ve submitted their thesis, in which case there might be an agreement that one of the supervisors take over as first author. Here, as with any other arrangement, the important bit is that it’s agreed up front and everyone is clear about what’s involved. 

Just to add, as a student, you should never be pressurised by a supervisor into letting them take the first author role. I’ve never seen this actually happen, but have heard stories of it; and if you feel under any coercion at all then do talk to your Course Director or another academic you trust.

The advantage of keeping your supervisor(s) involved is that they can then help you with writing up for publication, and that can be a major boost if they know the field and the targeted journal well. So use them: probably, the best way of getting an article published in a journal is by co-authoring it with someone who’s already published there. A way that it might work, for instance, is that you have a first go at cutting down your thesis into about the right size, and then the supervisor(s) work through the article, tidying it up and highlighting particular areas for development and cutting. Then it comes back to you for more work, then back to your supervisor(s) for checking, then back to you for a final edit before you submit.  

One final thing to add here: even though you may be working with people more senior and experienced to you, if you are first author on the paper, you need to make sure you ‘drive’ the process of writing and revising, so that it moves forward in a timely manner. So, for instance, if one of your supervisors is taking a while to get back to you, email them to follow up and see what’s happening; and make sure you always have a sense of the process as a whole. This can be tough to do, given the power relationship that would have existed if you were their supervisee; but, in my experience, the most common reason that efforts at publication fizzle out are because there’s no one really ‘holding’ or driving the process: no one making sure it does happen. Things fall through gaps: a supervisor doesn’t respond for a month or two, no one follows them up, the other supervisor wanders off, the student gets on with other things… So spend a bit of time, at the start, agreeing who’s going to be in charge of the process as a whole (normally the first author) and what roles other authors are going to have. And, if it’s agreed that you are in the driving seat, you’ve got both the right and the responsibility to follow up on people to make sure it all gets done.

How do you submit?

That takes us to the process of submitting to a journal.  So how does it work? Nearly all journals now have an online submission portal so, again, go to the journal website and that will normally take you through what you need to do. Submission generally involves registering on the site, then cutting and pasting your title and abstract into a submission box, entering the details of the author(s) and other key information, and uploading your papers. The APA 7th Manual has some great advice on how to prepare your manuscript so that it’s all ready for uploading (or see here), and if you follow that closely you should be ok for most journals.

You also normally need to upload a covering letter when you submit, which gives brief details of the paper to the Editor. This can also cover more ‘technical’ issues, like whether you have any conflicts of interest (have you evaluated, for instance, an organisation that you’re employed by?), and confirmation of ethical approval. If you’ve submitted, or published, related papers that’s also something you can disclose here. Generally, it’s fine to submit multiple papers on different aspects of your thesis, but they should be different; and it’s always good just to let the editor know so that it doesn’t come as a surprise to them later. 

Note, you definitely mustn’t submit the same paper (or similar papers) to more than one journal at any one time. That’s a real no-no. Of course, if your paper gets rejected it’s fine to try somewhere else (see below), but you could get into a horrible mess if you submitted to more than one journal in parallel (for instance, what happens if they both accept it?). So most journals ask you, on submission, to confirm that that’s the only place you’ve sent it to and that’s really important to abide by.  

What happens then?

The first thing that normally happens is that a publishing assistant will then have a quick look over your article to check that it’s in the right format. As above, they can be pretty pernickety here, and if you’re over the word limit, or not doing the right paragraph spacing, or even indenting your paragraphs when you shouldn’t, you can find your article coming back to you asking for formatting changes before it can be considered. So try and get it right first time.

Then, when it’s through that, it’s normally reviewed by the journal editor, or a deputised ‘action editor’. Here, they’re just getting a sense of whether the article is right for the journal, and at about the required level. Often papers will get rejected at that point (a desk rejection), with a standard email saying that they get a lot of submissions, they can’t review everything, it’s no comment on the quality of the paper, etc., etc. Pretty disappointing—and generally not much more feedback than that. Ugh!

If you don’t hear from the journal a week or so after submission, it generally means it’s then got through to the next stage, which is the review process. Here, the editor will invite between about two and four experts in the field to read the paper, and give their comments on it. This process is usually ‘blind’ so they won’t know who you are and you won’t know who they are. In theory, this helps to keep the process more ‘objective’: the reviewers aren’t biased by knowing who you actually are, and they don’t have to worry about ‘come back’ if they give you a bad review.  

The review process can take anything between about three weeks and three months. You can normally check progress on the journal submission website, where it will say something like ‘Under review.’ If it gets beyond three months or so, it’s not unreasonable to write to the journal and ask them (politely) how things are going. But there’s no relationship between the length of the time of the review and the eventual outcome—it’s normally just that one of the reviewers is taking too long getting back to them, and they may have had to look elsewhere. Note, even if it is taking a long time and you’re getting frustrated, you can’t send the paper off somewhere else until things are concluded with that first journal. You could withdraw the paper, but that’s fairly unusual and mostly people wait until the reviews are eventually back.

The ‘decision letter’

Assuming the paper has gone off for review, you’ll get a decision letter email from the editor. This is the most exciting—but also the most potentially heartbreaking part—of the publication process: a bit like opening the envelope with your A-level results in. Generally, this email gives you the overall decision about acceptance/rejection, a summary from the editor of comments on your paper, and then the specific text of the reviewers’ comments.

In terms of the decision itself, the best case scenario is that they just accept it as it is. But this is so rare, particularly in the better journals, that if you ever got one (and I never have), you’d probably worry that something had gone wrong with the submission and review process.

Next best is that they tell you they’re going to accept the paper, but want some revisions. Here, the editor will usually flag up the key points that they want you to address, and then you’ll have the more specific comments from the reviewers. Sometimes, journals will refer to these as ‘minor revisions’, as opposed to more ‘major revisions’, but often they don’t use this nomenclature and just say what they’d like to see changed. Frequently, they don’t even say whether the paper has been accepted or not—just that they’d like to see changes before it can be accepted—and that can be frustrating in terms of knowing exactly where you stand. Generally, though, if they don’t explicitly use the ‘r’ word (‘reject’), it’s looking good.

Then you can get a ‘reject and resubmit’. Here, the editor will say something like, ‘While we can’t accept/have to reject this version of the paper, due to some fairly serious issues or reservations, we’d like to invite you to resubmit a revision addressing the points that the reviewers have raised’. In my experience, about 60% of the time when you resubmit a rejected paper you eventually get it through, and about 40% of the time they subsequently reject it anyway. The latter is pretty frustrating when you’ve done all that extra work, but at least you’ve had a chance to rework the paper for a submission elsewhere. 

Then, there’s a straight rejection, where the editor says something fairly definitive like, ‘…. your paper will not be published in our journal.’ That’s pretty demoralising but, at least, if you’ve got to this stage, you’ve nearly always got some very helpful feedback from experts in this field to help you improve your work.

Emotionally, the editorial and reviewing feedback can be pretty bruising, especially when it’s a rejection. Reviewers don’t tend to pull punches: they say what they think—particularly, perhaps, because they’re under the cover of anonymity. So you do need to grow a fairly thick skin to stick with it.  Having said that, a good reviewer should never be diminishing, personal, or nasty.  Even when rejecting a submission, they’ll be able to highlight strengths as well as limitations, and to encourage the author to consider particular issues and pursue particular lines of enquiry, to make the best of their work and their own academic growth. So if something a reviewer says is really hurtful, it’s probably less about the quality of your work, and more about the fact that they’re being an a*$e (at least, that’s what I tell myself!).

Most journals do have some kind of appeal process if you’re really unhappy with the decision made. But you need a good, procedural argument for why you think the editorial decision was wrong (for instance, that it was totally out of step with the actual reviews, or that the reviewers hadn’t actually read your paper) and, in my experience, appeals don’t tend to get too far. However, I have heard of one or two instances of successful outcomes.

By the way, sometimes, quite quickly after you’ve started to submit papers (and possibly even before), you may be asked to review for the journal yourself. That can be a great way of getting to know the reviewing process better—from the other side. It’s also part of giving back to the academic community: if people are spending time looking at your work, it’s only fair you do the same. So do take up that opportunity if you can. There’s some very helpful reviewer guidelines here.  

Revising and resubmitting

If you’re asked to make revisions, journals will generally give you six months or so—less if they’re relatively minor. Here, it’s important to address every point raised by each of the reviewers. That doesn’t mean you have to do everything they ask for, but you do have to consider each point seriously, and if you disagree with what they’re saying, you need to have a good reason for it. Generally, you want to show an openness to feedback and criticism, rather than a defensive or a closed-minded attitude. If the editor feels like they’re going to have to fight with you on each point, they might just reject the paper on resubmission.

As well as sending back the revised papers, you’ll need to compile a covering letter indicating how you addressed each of the points that the reviewers’ raised. You may want to do this as a table as you go along: copy-pasting each of the reviewers’ points, and then giving a clear account of how you did—or why you did not—respond to that issue.

Pay particular attention to any points flagged up by the editor. Ultimately it will be their decision whether or not to accept your paper, so if they’re asking you to attend to some particular issues, make sure you do so. 

Resubmissions go back through the online portal. If the changes required are relatively minor, it may just be the editor looking over them; anything more substantive and they’ll go back to the reviewers again for comment. Bear in mind that the reviewers are often the original ones who looked at your paper, so ignore their comments at your peril.

It’s not unusual to have three or four rounds of this review process: moving, for instance, from a ‘revise and resubmit’ to ‘major revisions’ to ‘minor changes’. At worst, it can feel petty and irritating; but, at best, and far more often, it can feel like a genuine attempt by your reviewers to help you improve the paper as much as possible. The main thing here is just to be patient and accept that the process can be a lengthy one. If you’re in a rush and just desperate to get something out whatever it’s quality, you’re likely to be profoundly frustrated—unless you’re prepared to accept publication in a journal of much lower quality.  

Once it’s accepted

Yay! You got there! That’s it… not quite. It’s brilliant to have that final acceptance letter from the journal telling you that they’ll now go ahead and publish your paper, but there is still a little more to do. A few weeks after the acceptance email, they’ll send you a link to a proof of the paper, where there’ll be various, relatively minor copy-editing corrections and queries. For instance, they may suggest alternate wording for sentences they think could be improved, or ask you to provide the full details for a reference. Sometimes, this may be in two stages: with, first, a copy-edited draft of your manuscript, and then a fully formatted proof). Note, at this point, they really don’t like you to make any substantive changes, so anything you want to see in the final published article should be there in your final submitted draft.

Then that it is. Normally the paper will be out, online, a week or so after that. And once it is, you can finally celebrate, but do also make sure you let people know about the paper, and give everyone the link via social media. The journal, itself, are unlikely to do any specific promotion of the article, so it’s up to you to tell colleagues about it and encourage them to let others in the field know.

Open Access?

Although it’s great you’ve got your paper out, the final pdf version may only be available to people who have access to the journal. So students at higher education institutes are likely to be fine, as are colleagues working for large organisations like the NHS, but what about counsellors or psychotherapists who don’t have online access, and where the cost of purchasing single articles are often prohibitively high? One possibility is that you (or the institution you are affiliated to) can pay to make your article ‘open access’. However, this can cost £1000s (unless the University has a pre-established agreement with the publisher) and is not something most of us can afford.

Fortunately, journals normally allow you to post either your original submission to the journal (an ‘author’s original manuscript’, or ‘preprint’ version of your article), or your final submission (a ‘prepublication’, ‘author final’, ‘postprint’, or ‘author accepted manuscript’ version of your article) on an online research depository, such as ResearchGate. Policies vary, so check the specific policies for the journal that published your paper:

• APA: Internet Posting Guidelines

• Wiley: Self-Archiving Policy

• Taylor and Francis: Preprint Policy

• Sage: Author Archiving and Re-Use Guidelines

This version of your paper won’t be the exact article that you published, and it won’t have the correct pagination etc., but if you prepare it well (see an example, here), then it means that those who don’t have access to journal sites can still find, read, and cite your research. Different journals do have different policies on this, though, so make sure you check with the specific publisher of your journal before making any version of your paper publicly available. Generally, what the publishers are very vigilant about is the making available, in a public place, of the final formatted pdf of your paper (unless, as above, it’s specifically open access).

Trying elsewhere

If your paper gets rejected, your choices are (a) just to give up, (b) resend the paper as is it somewhere else, or (c) make revisions based on the feedback and then resubmit elsewhere. There’s also, of course, a lot of grey areas between (a) and (b) depending on how many changes you feel willing—and able—to make. Generally, if you can learn from the feedback and revise your paper that’s not a bad thing, and can help form a stronger submission for next time. Of course, it is always possible that the next set of reviewers will see things in a very different way; and sometimes changes made to address one set of concerns will then be picked on by the next set of reviewers as problems in themselves. As for (a), well, I promise you this: if the research is half-decent, then you can always get it published somewhere. Bear in mind that, as above, if you’ve been awarded a doctorate for your research (and, to some extent, a Master’s), it’s publishable by definition. 

Generally, when people get their papers rejected, they move slowly down the impact hierarchy: so to journals that might be more tolerant of the ‘imperfections’ in your paper. But there’s no harm in trying journals at a similar level of impact when you’re trying somewhere else or even higher up—particularly when you really don’t agree with the rejecting journal’s feedback.

Ultimately, it’s about persistence. To repeat: if you want to get something published, and it’s passed at doctoral (or, often, Master’s) level, you will. But it needs resilience, responsiveness, and a willing to put up with a lot of knockbacks.   

Other pathways to impacts

Journals aren’t the only place where you can get your research out to a wider audience and make an impact. For instance, you could write a synopsis of your thesis and post it online: such as on Researchgate. You won’t get as big a readership as in an established journal, but at least it will be more accessible than your university library, and you can tell people about it via social media. Or you could do a short blog about your research, or make a video, or talk to practitioners and other stakeholders about your work. If you want to make your research findings widely accessible to practitioners, you could also write about them for one of the counselling and psychotherapy magazines, like BACP’s Therapy Today or BPS’s The Psychologist.   

There’s also many different conferences that you can go to to present your findings: as an oral paper, or simply as a poster. Two of the best, for general counselling and psychotherapy research in the UK, are the annual research conference of the British Association for Counselling and Psychotherapy (BACP), and the annual conference of the BPS Division of Counselling Psychology (DCoP). Both are very friendly, encouraging, and supportive; and you’ll almost certainly receive a very warm welcome just for having the courage to present your work. At a more international level is the annual conference of the Society for Psychotherapy Research (SPR). That’s a great place to meet many of the leading lights in the psychotherapy research world, and is still a very friendly and supportive event. 

You can also think about ways in which you might want your work to have a wider social and political impact. Would it make sense, for instance, to send a summary to government bodies, or commissioners, or something to talk to your local MP about?

Of course, this could all be in addition to having a publication (rather than instead of it), but the main point here is that, if you want your research to have impact, it doesn’t just have to be through journal papers.  

To conclude…

When you’ve finished a piece of research—and particularly a long thesis—often the last thing you’ll want to be doing is reworking it into one or more publications. You can’t stand the sight of it, never want to think about it again—let alone take the research through a slow and laborious publication process. But the reality is, as people often say, the longer you leave it the harder it gets: you move away from the subject area, lose interest; and if you do want to publish at a later date, you’ll have to familiarise yourself with all the latest research (and possibly without a library resource to do so). So why not just get on with it, get it out there; and then you can have your work, properly, in the public domain, and people can use it and learn from it, and improve what they do and how they do it. And then, instead of spending the next few decades wishing you had done something with all that research, you can really, truly, have the luxury of never having to think about it again.

Acknowledgements

Many thanks to Jasmine Childs-Fegredo, Mark Donati, Edith Steffen, and trainees on the University of Roehampton Practitioner Doctorate in Counselling Psychology for comments and suggestions. 

Further Resources

There is a great, short video here from former University of Roehampton student, Dr Jane Halsall, talking about her own experience of going from thesis to published journal paper. Jane concludes, ‘You’re doing something for the field, and you’re doing something for the people who have actually taken the time out to participate. So be encouraged, and do do it.’

An accessible set of tips on publishing in scholarly is also available from the APA:

• Part 1: the Publishing Process

• Part 2: Role of the Editorial Board

• Part 3: Peer Review

Disclaimer

The information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

The Viva: Some Pointers

The following blog is for Master’s or doctoral level students writing research dissertations in the psychological therapies fields. The pointers are only recommendations—different trainers, supervisors, and examiners may see things very differently.

Many thanks to Jasmine Childs-Fegredo, Mark Donati, and Edith Steffen for comments and suggestions.

 ***

For doctoral students, the viva is the endpoint of your academic journey, and can be the most dreaded part.  So what is it, and what should you do to make it go as well as possible?

The Set Up

Typically, you’ll have two examiners: an ‘internal’ (someone based at your university), and an ‘external’ (someone based at another university).  The external usually carries more weight, and may have more influence on the final decision.  You may also have a ‘Chair’ (normally someone based at your university as well), but their role will just be to manage the viva examination.  They don’t have a role in assessing you.

 Often, you can choose whether or not to have your supervisors present at the viva, though they won’t be able to say anything.  This can feel like moral support, and they can take notes on what might need to be revised.  However, you may also feel more pressure having additional people in the room.

Typically, a viva lasts for about 90-120 minutes, though that can vary a lot.  If longer, you’ll normally get a short break.

What viva examiners often do is to go through your thesis chapter by chapter, asking questions and discussing with you aspects of your work along the way.  Sometimes your examiners will take it turns to ask questions, or the external may take more of a lead.  However, this can depend on the examiners’ areas of expertise.  For example, if your external knows more about your methods, and your internal more about your content area, they may divide the questions up in that way.

Prior to the viva, both of your examiners will have read through your thesis, and written an independent report of what they make of it, and approximately what outcome they think you should be awarded.  In the vast majority of cases, this will be either ‘minor amendments’ (for instance, adding more on reflexivity, discussing the limitations in more depth) or ‘major amendments’ (for instance, restructuring the literature review, revising the analysis).  In a small number of cases, they may also feel that you need to collect more data—a very major amendment.  It’s also possible that they’ll feel the thesis should fail but, thankfully, that’s very rare, and something that your supervisors would normally alert you to before you submit.  Equally rare is that the examiners will just pass your thesis without wanting to see any changes at all, so it may be best to go into the viva assuming that the examiners will ask you to make revisions to some degree—even if it’s just correcting typos.  Before they meet you, your examiners will also have met with each other and shared their views on your thesis, coming up with a list of questions to structure the viva by.

Your examiners may start by telling you their overall assessment of your thesis, or they may not.  If this doesn’t happen, don’t read anything into it—some examiners just prefer not to do so.

After they’ve talked your thesis through with you, the examiners will ask you to leave the room (for 30 minutes or so), and then they’ll discuss with each other what they think the outcome should be and what changes they think you should make.  Then they’ll invite you back in and share the result with you.  If, as normal, they’re asking for some amendments, they’ll go through them with you but you won’t need to write them down, as you’ll be sent the feedback in writing soon after the viva.

What’s it For?

As an external examiner, what I’m wanting from the viva is three things.  First, I want to make sure that the student has really written their thesis, and not got someone else in to do it for them.  So that means I’m looking to see that they can talk about their work in a fairly fluent and knowledgeable way.  Second, although I’ll come into the viva with an outcome in mind and some idea of the kinds of amendments that I might want to see, I’m also open to revising that, depending on how the candidate talks about their work.  For instance, I might feel that they should have conduct a systematic literature review rather than a narrative one, but if they present a convincing argument for why they did the latter, then I may be happy to let that go.  Third, I might want to convey—and explain—to the student why I think they should make certain changes to their thesis, and what those changes are.  

 Remember that your examiners, like your supervisors, will almost certainly want to see you get through.  No one wants to fail anyone—we all know how much work a thesis takes.  But we also will want to make sure things are fair: if it feels like you haven’t got your head around certain things, or done the work that you’ve needed to do, then it wouldn’t feel right to pass you alongside others.  And we’re also aware that your thesis will be lodged publicly, for all to access and read.  So we want to see it in the best shape possible: something you can be proud of and that reflects the best of your abilities.

How to Prepare

Before the viva, have a really good few read throughs of your thesis so that you know it well.  You may have completed it several months before the viva, so it’s important to re-familiarise yourself with it—particularly the more tricky or complex parts.

Practice vivas are essential.  Your supervisor(s) will often be willing to do this with you.  If not, or as well as, do practice vivas with your peers or friends.  Get them to ask you questions about your thesis—particularly the more difficult bits (like epistemology, or your choice of methods, or any statistical tests) so you can get practised at talking these elements through.  Talk to your friends, your family, your cat about your thesis (as much as they can bear it) so that you’re really familiar with what you did and why.

What to Take to the Viva?

One of my personal bugbears, as an examiner, is when students come to a viva without a copy of their own thesis, and then have to borrow mine to answer questions.  So make sure you bring yours along, with sections clearly marked so you can find your way around it when asked about different parts.  It’s fine also to bring a notepad so you can write down questions.

Nerves

It can be really scary doing a viva, and your examiners should be well aware of that and sensitive to it—bear in mind that they will have gone through one of their own.  So if you get really nervous at the start or during the viva, it’s normally fine to ask for just a bit of time to compose yourself—there’s no rush. You may even want to let the Chair or examiners know at the start, if you think that will help. 

What Will They Ask Me?

Mostly, the questions that your examiners will ask will be specific to your particular thesis.  As indicated above, typically, they’ll go through it chapter by chapter, and ask you to explain, or elaborate on, specific aspects of your work.  The questions will often be on the areas that they feel might need further work.  However, if they feel that really not much needs to be changed, they may just be asking about particular areas of interest to discuss them with you.  After they’ve asked you about a particular area of issue, they may follow this up with further questions or prompts.  Questions may be fairly general (for instance, ‘Can you explain your choice of analytical method?’) or very specific (for instance, ‘On page 125, you indicate that the p-value was .004, but on page 123 you write that the regression analysis wasn’t significant, can you explain that please’).  There’s also some standard questions that examiners may ask, for instance:

•  Why did you choose to do this study?

• How did you go about choosing what literature to look at?

• What was the underlying epistemology for your research?

• What was the rationale for your sample?

• Why did you choose this particular method?  Why not xxx method?

• What are the implications for counselling/psychotherapy/counselling psychology practice of your thesis?

• What does your research add to the field?

• What are the limitations of your study?

• What was the impact of your personal perspective on the study? Biases?

• What did you personally learn from the study?

Elaborate, Elaborate, Elaborate

In terms of the actual viva, the main bit of advice I would give candidates is to make sure you really elaborate on your answers.  Of course, you want to stay on track with the particular question you’ve been asked, but don’t be too short or pithy in how you respond.  For a typical viva, the examiners may have prepared, say, 10 questions or so, so you need to talk on each area for, perhaps, 10 minutes; and you don’t want a situation where your examiners are constantly having to pump you for answers.  This is your chance to show your depth and breadth of thinking so, for instance, reflect with the examiners on why you made the choices you did, show how you weighed up different possibilities, talk about the details of what you considered and what you found.  Ultimately, what your examiners want to see is that you can think deeply and richly and complexly about things—rather than that you have reached any single definitive conclusions.  So it’s less about getting it ‘right’, and more about showing all the thinking that has been going on. 

Don’t be Defensive

The other main thing I would say is not to be too defensive when you respond to the examiners’ questions and prompts.  As indicated above, they’ll have a view on what they may want you to revise in your thesis, and while you may be able to change their minds to some extent, you don’t want to come across as too rigid or stubborn in your thinking.  If, when they point something out to you, you think, ‘Actually, they’re probably right,’ that should be fine to say, and better than trying to defend something that you can clearly see is in need of adjustment.  Of course, if you think you’re right, do say it and say why, but you don’t have to defend to the bitter end every element of your work.  Better to show, like all of us, that you can sometimes get things wrong and that you’re open to learning and improving.

Be the Expert You Are

As Mark Donati, Director on our Doctorate in Counselling Psychology at the University of Roehampton suggests, don’t be afraid to express your opinion and say what you really think.  Of course, it’s best if this is based on the available evidence; but sometimes the evidence just isn’t available, and then the examiners may be really interested in your ‘best guess’ of what’s going on.  Remember that you are the expert in the area now.  That’s right, you are.  And the examiners may be really excited to hear from you what the view is from the leading edge of the field. 

Don’t Shame your Examiners

That might sound strange to say, but bear in mind that your examiners are also in a social situation, and may be experiencing their own pressures to ‘perform’.  Dr X, for instance, has come down from University Y, and it’s the first time they’ve met your internal examiner Professor Z, whose work they’ve always admired, as well as Chair W, who they don’t know very well but who seems an important figure.  So Dr X wants to show that they’ve got a good understanding of your work, with some intelligent questions to ask, and some good insights about the field.  What that means is, if you want to keep your examiners ‘on side’, treat them with respect and show an interest in what they’re saying and the questions they asked.  You really don’t want to respond to Dr X in a way that may make them feel foolish in front of Professor Z, or like they have to defend themselves.  What this also means is that some of what goes on in the room may not be about you, but also about the dynamics between the rest of them. 

Enjoy

It’s easier said than done, but if you can enjoy your viva (and many students do end up doing so) then that’s great.  Think of it this way: you’ve got a captive audience for two hours who you can talk to about all the work you’ve been doing for the last few years.  And now you’re the expert, so make the most of it: tell them about what you’ve been really thinking, and about some of the complex challenges doing the thesis, and about all your ideas about where the research should go for the future.  It’s your chance to shine, and if you can really connect with your energy and enthusiasm for your work, your examiners are sure to appreciate that—and so might you.

Presentations: Some Pointers

Present. Why? Because it’s a great way of getting your work out there: letting people know what you are doing, opening up conversation, getting feedback. When you present, you enter into dialogues with your community: people who can help you, encourage you, give you new ideas.

It’s scary. I know. I used to be absolutely phobic about presenting. I used to think, ‘What happens if I just clam up in front of all these people. Just stand there, dumbstruck, with all those eyes on me. Nowhere to go.’ But I did, really, push myself to present: to go for opportunities even if I knew I’d be terrified. And over time (albeit more time than I would have liked), it began to get easier.

For counselling and psychotherapy researchers, a great place to present your work is the annual research conference of the British Association for Counselling and Psychotherapy. It’s low key, friendly, and audiences are always really encouraging of people’s work. For counselling psychologists, another great opportunity to present is the BPS Counselling Psychology annual divisional conference.

Normally when you do a presentation, there will be a ‘Chair’ who will make sure you start and end on time, and possibly introduce you.

Research presentation are normally around 20 minutes, and then around 10 minutes for questions and discussion. But each conference will have their own guidelines.

Generally, conference delegates can pick and choose what they go to, and there’s likely to be a few strands of presentations running at once. So it hard to predict how many people will come to your talk, but it’s likely to be somewhere between about 10 and 50.

Research papers can either be presented individually, or as part of a ‘symposium’ (sometimes called a ‘panel’), where papers on a similar theme are grouped together. Normally, you can either submit as an individual paper or as part of a symposium—but if you do have colleagues doing similar work, creating a symposium can make for a more coherent set of presentations.

Prepare… prepare… prepare…

• Know your timing: check that the length of your presentation fits into the allocated time slot. Be particularly wary of having much too much material for the time available.  Keep an eye on the time during your presentation and, if helpful, write on your notes where you should be up to by particular points, so you know if you need to speed up/slow down.

• Practice your slides to get a good feel for them, and so you know what’s coming next.

• Turn up to the room early and check your slide show is uploaded and works. Know the pointer, how to change slides, etc. Technological issues are often the biggest saboteur of a good presentation.

• Try to introduce yourself to the Chair before you start (if there is one), and check how they are going to run things (in particular, how/whether they will let you know how much time you have left).

• If you get anxious doing talks, think about how you could manage that. For instance, do you need things written out in detail to fall back on, or have breathing techniques ready if you get panicky?

• Presenter View on Powerpoint can be a really helpful tool for being on top of your presentation. Essentially, it means that, when you present, you (and only you) can see what slides are coming up, and also any notes on your slides. It can be a bit technologically fiddly though.

• Presenter View or not, it’s generally best to take along a printed off copy of your slides (say, 3 slides to a page), so that you can always quickly check content on other slides when you are doing presentation, and just in case the technology breaks down.

A great short video on what happens when you fail to prepare a presentation, and everything else you can do wrong, can be found here.

Slides

• Keep the lines of texts per slide to a minimum. Generally no more than 6-10 lines of text per slide. If you have more to say, do more slides, they don’t cost anything! (I do really mean this one: so many presentations I see have 20+ lines of texts per slide, making the slide pretty ineligible).

• Related to the above, font size shouldn’t normally be less than 30 points, and definitely not less than 16-20 points.

• Texts should be bullet points, rather than complete sentences (so don’t have full stops at the end of them). Your bullet points should capture the essence of what you want to say (which you can then expand upon verbally), rather than spelling the point out in full.

• Try to avoid

  • Sub bullet points,

    • And sub-sub bullet points.

      • The slides start to get very messy.

• Be consistent in your formatting: e.g. fonts, type of bullets, colour of headings.

• If you have text on your slides, talk ‘to’ it. Don’t have text on the slide that you never refer to. (Though it’s OK to say things that aren’t on your slide).

• Use the space on the slides—make text large rather than small text squashed away.

• You don’t need line spacing between your bullet points. If you take those out you can make your font larger.

• Try to avoid too many citations in your bullet points as they can be distracting. You can cite sources at the bottom of the page or have a page of references at the end of the presentation if people want to follow up. Having said that, if you’re discussing a key text, make sure you give a reference so that your audience can follow up.

• Sans serif fonts (e.g., Arial, Tahoma, Century Gothic) are generally more suited to presentations than serif fonts (e.g., Times New Roman, Palatino). NCS: Never Comic Sans!

• Try to use images/graphics wherever possible, ideally each slide.  You can also embed videos (but check sound works before your presentation). Images and videos can be a great way of conveying the reality of your research: for instance, a photo of the room where the interview took place, or a short video of you doing the coding (bear in mind confidentiality, of course).

• Diagrams can be really helpful, but do make sure you spend time talking them through and explaining what different elements mean. Don’t just leave it up to your audience to work it out for themselves.

• Don’t make slides too complex/‘flashy’: for instance, by using transition sounds.  Everyone hates transition sounds!

• Having said that, a simple transition between slides, like ‘Fade’, can be a nice way of going from slide to slide.

• ‘Animations’ allow you to present one bullet point at a time, and can be helpful for ensuring that you and your audience are on the same points. Again, though, just use simple entrance animations, like Fade, so that it doesn’t detract from your content.

• For a research presentation, it’s generally fine to use the standard sections of a research paper to structure your talk: Introduction (including literature review), Aims, Methods, Results, Discussion. Headings can be on separate slides to keep the sections really clear.

• Give clear titles to each slide so that the audience know what you are trying to say.

• Don’t scrimp on presenting your results: they’re often the most important and interesting part of your paper, so ensure you leave a proper amount of time to talk through them (say 50% of your overall time, if a qualitative presentation).

• Everyone uses Powerpoint—think about trying Prezi.

• Watch copyright—you shouldn’t use images that aren’t in the public domain. You can find many images that are available for reuse via Google Search/Images/Settings/Labelled for reuse.

 ConnectING with your audience

• This is the key to everything: talk to your audience. Try to connect with them. Imagine, for instance, that they are a friend that you really want to explain something to. You’re not trying to be smart, or clever, or get them to approve of you—you just want to explain something to them about what you’ve done, what you’ve found, and what it means. So breathe, focus, speak to the people in the room (or online). Try not to just rattle through what you have to say.

• That means trying, yourself, to connect with the ‘story’ of what you are saying: if it’s meaningful to you it’s more likely to be meaningful to your audience.

• Remember that, nearly always, your audience are there to learn from you—not to judge you. They haven’t come along to your presentation thinking, ‘Hmm, I wonder if [insert your name here] is a good presenter or not. I’d really like to know.’ In fact, the harsh truth is that they’re almost certainly not thinking much about you at all. Rather, they’re thinking, ‘Hmm… I’d be interested to know more about [insert your topic here]’. So the question you should be asking yourself is not ‘How can I prove I’m good enough?’ but, ‘What can I teach these people?’

• Lead your audience through your talk. You may be really familiar with your material, but they are unlikely to be. So explain things properly: from why you did your research, to what your findings mean, to what it says, ultimately, about clinical practice.

• Know who your audience is and adjust accordingly. For instance, a group of experienced practitioners may know, and want, very different things from a group of early stage researchers. Think about what your audience will want from the talk. And what they might already know (that you don’t need to repeat)?

• Try not to read directly from your notes, or from your slides. Best to use them as stimuli.

• Avoid jargon or lots of acronyms. Keep it as clear and easy to understand as you can. If you need to use acronyms, explain clearly what they mean.

• Speak loud and clear—check people can hear you, if need be, particularly at the back.

• Watch that you’re not talking too fast, particularly if you’re anxious. Try the talk out with a friend/colleague and get some honest feedback from them.

• Pace your talk, so that you have enough time for all of it. It’s a classic mistake to get very caught up in the first part of your talk, and then have to rush the rest (and often the most interesting bits).

• Make sure you leave time for questions—so that you’re audience can really engage with you.

• Don’t be defensive if asked questions: accept that there may be things to develop in your paper if you can see that.

• It’s really bad form to run over time, as it means you’re eating into the next person’s allocated slot (or everyone’s coffee/lunch). So if you’re asked to stop, stop. (I once saw a presentation where the speaker, already running 30 minutes over time, starting asking the audience whether or not they thought he should be hauled off. Very, very awkward!)

• It’s fine to bring yourself in to the presentation, and often that’s a way of helping the audience connect with you. For instance, why did you, personally, want to do this study? What did you, personally, get out of it?

• Humour can be a great way of connecting, and cartoons can often lighten a talk and engage and audience. But don’t force humour if it’s not there or if it’s not ‘you’.

• And, finally, don’t stand in front of the projector!

Posters

If you’re not keen on presenting a paper orally, you can always present a ‘poster’. That can be particularly appropriate if your work is still in progress. And it’s another great work of initiating dialogue around your work with other members of the counselling community.

DISCLAIMER

 The information, materials, opinions or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

The Discussion Section: Some Pointers

The following blog is for Master’s or doctoral level students writing research dissertations in the psychological therapies fields. The pointers are only recommendations—different trainers, supervisors, and examiners may see things very differently.

The aim of a discussion section is to discuss what your findings mean, in the context of the wider field.

As with all other parts of your dissertation, make sure that your Discussion is actually discussing the question(s) that you set out to ask.

It’s really important that your Discussion doesn’t just re-state your findings (aside from a brief summary at the start). It’s often tempting to reiterate results (just in case the reader didn’t get them the first time!), but now’s the time to move on from your findings, per se. Structuring your Discussion in a different way from your Results can be a good way of trying to ensure this. So, for instance, if you’ve presented your Results by theme, you might want to structure your Discussion by stakeholder group or by research questions.

Generally, you shouldn’t be presenting raw data in your Discussion: for instance, quotes or statistical analyses. That goes in your Results.

Similarly, try to avoid referencing lots of new literature in your Discussion. If it’s so relevant, it should be there in your Literature Review.

Make sure that your Discussion does, indeed, discuss your findings. It shouldn’t just be the second half of your Literature Review: something which bypasses your own research. Emphasise the unique contribution that your findings make, and focus on what they contribute to knowledge. Be confident and don’t underplay the importance of your own findings.

At the same time, don’t over-state the implications of your findings (particularly with regard to practice). Be realistic about what they mean/indicate, in the context of the limitations of your study, as well as its strengths.

This is your chance to be creative, exploratory, and to investigate specific areas in more detail, but try to ensure that it’s always grounded in the data: what you found or what others have found previously. So not just wild speculation.

What’s unexpected in your results? What’s surprising? What’s counter-intuitive? What’s anomalous? Your Discussion is a great opportunity to bring these out to the fore more fully and explore them in depth.

Typical sections of a discussion section (often in approximately this order)

• Brief summary of your findings (but keep it brief—just a concise but comprehensive paragraph or two).

• What your findings mean, in the context of the previous literature. So, for instance, how they compare with/contrast/confirm/challenge previous evidence and theory. This is also an opportunity for you to untangle, and to try and explain, complex/ambiguous/unexpected findings in more depth.

  • This would normally be the bulk of your Discussion. It may be appropriate to structure this section by your research questions, or by the themes in your results. If you do the latter, though, as above, be careful that you’re not just reiterating your findings.

  • Remember that you don’t need to give equal weight/space to all your findings. If some are much more interesting/important than others, it’s fine to focus your Discussion more on those; though all key findings should be touched on at some point in the Discussion.

• Limitations. This should be a good few paragraphs. Try to say how the limitations might have affected the results (e.g., ‘a volunteer sample means that they may have been more positive than is representative’) rather than just what the flaws in the study were, per se.

  • Be critical of what you did; but from a place of reflective, appreciative awareness, rather than self-flagellation. The point here is not to beat yourself up, but to show that you can learn, intelligently; just as you did something, intelligently.

• Implications for clinical practice. Also, if relevant, implications for policy, training, supervision, etc.

  • Try to keep this really concrete: what would someone do differently, based on what you found.  So, for instance, not just, ‘These findings may inform practitioners that….’ But, ‘Based on these findings, practitioners should….’

• Specific implications for your specific discipline: e.g., counselling psychology/counselling/psychotherapy.

• Suggestions for further research.

• Reflexivity: what have you learnt from the study, both in content and in practice.

Conclusion: this can be a brief statement bringing all your thesis together.

Appendices

Following your references, you are likely to want to append various documents to your thesis. These can include:

• Participant-facing forms: e.g., information sheets, consent forms, adverts.

• Full interview schedule.

• Additional quantitative analyses and tables.

• A transcript of one interview (but bear in mind confidentiality—this may not be appropriate). This could also show your coding of that interview.

• All text coded under one particular theme/subtheme, for the reader to get a sense of how you grouped data together (again, bear in mind confidentiality).

(Image by Muhammad Rafizeldi, Creative Commons Attribution-Share Alike 3.0 Unported license)

The Methods Section: Some Pointers

The following blog is for Master’s or doctoral level students writing research dissertations in the psychological therapies fields. The pointers are only recommendations—different trainers, supervisors, and examiners may see things very differently.

What should go into the Methods chapter of a thesis, and how much should you write in each area? The headings, below, describe the typical sections, content areas, and approximate length . The suggested word lengths are in the context of a 25,000-30,000 word thesis, and may be a bit more expanded for a longer dissertation (and obviously more condensed for a shorter one).

Epistemology

(Approx. 2,000-3,000 words).

This is often a requirement of Master’s or doctoral level theses, and is a key place in which you can demonstrate the depth and complexity of your understanding. This may be a separate chapter on its own, or placed somewhere else in the thesis.

• Critical discussion of epistemology adopted (e.g., realist, social constructionist)

• Links to actual method used

• Consideration/rejection of alternative epistemologies. 

Design

(Approx. 50-500 words).

• Formal/technical statement of the design: e.g., ‘this is a thematic analysis study drawing on semi-structured interviews, based in a critical realist epistemology’

• Any critical/controversial/unusual design issues that need discussing/justifying.

Participants

(Approx. 500 words).

• Site of recruitment: Where they came from/context

• Eligibility criteria: inclusion and exclusion

• Demographics (a table here is generally a good idea: can by one participant per row if small N, or one variable per row if large N)

  • Gender

  • Age (range/mean)

  • Ethnicity

  • Disability

  • Socioeconomic status/level of education

  • Professional background/experience: training, years of practice, type of employment, orientation

• Participant flow chart/description of numbers through recruitment: e.g., numbers contacted, number screened, numbers consented/didn’t consent (and reasons). Also organisations contacted, recruited, etc.  

Measures/Tools

(Approx. 500 words).

• Interview schedule

  • Nature of interviews: e.g., structured/semi-structured? How many questions?

  • Give key questions

  • Prompts?

  • (Full schedule can go in appendix)

• Measures (including any demographics questionnaire): a paragraph or two on each

  • Brief description

  • Background

  • What it is intended to measure

  • Example item(s)

  • Psychometrics:

    • reliability (esp. internal reliability, test/retest)

    • validity (esp. convergent validity)

Procedure

(Approx. 500-1000 words).

• What was the participants’ journey through the study: e.g., recruitment, screening, information about the study, consent, interview (how long?), debrief, follow up

• Nature of any intervention: type of intervention (including manualisation, adherence, etc), practitioners…  

Ethics

(Approx. 500 words).

• Statement/description of formal ethical approval

• Key ethical issues that arose and how they were dealt with 

Analysis

(Approx. 1,000-2,000 words).

• What method used

• Critical description of method (with contemporary references)

• Rationale for adopting method

• Consideration/rejection of alternative methods

• Stages of method as actually conducted (including auditing/review stages) 

Reflexive statement

(Approx. 250 words).

Remember that the point of your reflexive statement here is not to give a short run-down of your life. It’s about disclosing any biases or assumptions you might have regarding your research question. We will all have biases, and by being open about them you can be transparent in your thesis and all the reader, themselves, to judge whether your results might be skewed in any way.

• What’s your position in relation to this study?

• What might your biases/assumptions be? 

The Literature Review: Some Pointers

A video based on this blog filmed with Rory at Counselling Tutor

Aims

The purpose of a literature review is to bring together what is known, so far, in relation to the question(s) being asked. So, for a decent literature review, the first thing is to be really clear about its aims and the questions you are asking (see Research aims and questions: Some pointers).

A literature review is not an essay. When people write an essay, what they generally do is to draw together various bits of theory and research to try and make one (or several) points. An essay is about constructing an argument and then justifying it. But a literature review is different. You’re not trying to make a point in it or prove something you already believe in. Rather, you’re asking a question and then trying to answer it by searching out all the relevant literature in relation to that question. If you know the answer to your question(s) before you’ve done your literature review then something is not quite right. A literature review, as with all research, should be based on answering a question you don’t know the answer to.

The Scope of a literature review

From degree level to Master’s level to doctoral level (Levels 6, 7, and 8, respectively, in the QAA Frameworks for Higher Education Qualifications), a literature review should demonstrate a systematic understanding of some element of a particular field. In addition, from Master’s to doctoral level, this should be increasingly at the forefront of a discipline and creating original knowledge; and, at doctoral level, meriting journal publication. To achieve all this, it means that your research question(s) needs to be focused and narrow enough to allow for a systematic understanding.  If there’s too much literature on your question to know it all, your question is probably too broad—try narrowing it down.  

Ask yourself, ‘What might I feel confident in saying that I systematically understand, that I can be a leading expert on?’  If that feels way above what you can achieve, narrow your focus down until it’s really possible for you to believe you’re a leading expert in it. So, for instance, if you’re asking a question like, ‘What is the relationship between empathy and therapeutic outcomes?’ you’ll soon find out that it’s going to take a lifetime to lead expertise here: there’s hundreds of research papers on it. But the relationship between self-disclosure and therapeutic outcomes in person-centred therapy—there’s maybe a dozen or so key papers here that means that some level of leading expertise is within your grasp. 

Remember—particularly for Master’s and doctoral level—you also need to be at the forefront of a field.  Not what was talked about 20 years ago, but what is being discussed and debated now.  If you find most of your references are back in the 1980s and 1990s, think about why there’s nothing more current.  Is it that people have stopped being interested in this question?  Is it that you’ve missed the latest research?

At Master’s level, you need to demonstrate mastery of a field.  That is, not just that you know the literature, but that you can do things with it: e.g., evaluate the reliability of different sources of evidence, compare, and contrast ideas. At doctoral level, you should be able to demonstrate, not only mastery, but an ability to do things with the literature in independent and original ways: e.g., come up with new interpretations and perspectives. So at both Master’s and doctoral level, you need to be able to go beyond simply describing relevant literature or findings, towards producing a synthesised understanding of the current state of knowledge in relation to your research questions.

Be critical.  This doesn’t mean insulting or attacking specific pieces of work—e.g., ‘What a tw*t Smith (2007) is for saying…’—and it doesn’t mean finding flaws in research for the sake of it. What it means is being able to extract from the literature what is relevant to your own research question(s), and to evaluate its importance to you.  That might mean, for instance, saying that the participants in a particular study were all White, so the findings may not be generalisable to people of other ethnicities; or that the use of quantitative methods means that we don’t really understand the mechanisms of change.

It’s not the end of the world if there’s one or two or papers that you’ve missed. Everyone misses things, and your examiners/assessors are likely to understand. But try to avoid having big gaps in your review, where whole areas of literature have been overlooked. That’s where systematic reviews can really come in handy.

doing a literature review systematically

Systematic literature reviews are reviews of the literature that have a series of explicitly-stated stages. This might include specifying your search terms, reporting on your ‘hits’, and systematically analysing your findings. They also focus on answering an explicitly-stated question. Different teaching programmes have different requirements about whether a literature review should be ‘systematic’ or not but, often, it’s an indication of higher quality, robustness, and transparency. However, there’s not one form of a systematic literature review and, in general, it can be considered on a spectrum: from highly systematic reviews (including, for instance, multiple coders, see below), to reviews with some systematic elements (such as an explicitly-articulated search strategy). A literature review may also have one or more systematic sections, rather than being a systematic literature review in its entirety. For instance, you might start a literature review by exploring a particular area, identify a question that seems of importance, and then go on to conduct a systematic review of what is known in relation to that question.

Ideally, the stages of a systematic literature review are set out before you start as a written protocol. You can see an example of one here, which we developed to examine the factors that facilitated and inhibited integration in child mental health services (see published paper here). This protocol covers such areas as:

• Aims

• Eligibility criteria for studies (i.e., which studies you’ll accept for review)

  • Study characteristics (e.g., only empirical studies, only studies of young people)

  • Report characteristics (e.g., only studies after 1990, only English language)

• Information sources (i.e., where you’ll look for studies, see below)

• Study selection procedures

• Planned method of analysis

Feel free to use the headings from our protocol for your own review.

There’s a very well-established set of guidelines that set out standards and expectations for reviews (particularly quantitative ones), the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA). All the elements detailed here aren’t normally considered necessary for a Master’s or doctoral level review, but even if you don’t do a full systematic review, you may want to draw on certain parts (such as a ‘flow chart’ of the references you used, see below).

At minimum, for any kind of literature review, it is generally useful to show how you went about ensuring that you identified relevant literature in your area. For instance, you could include your search terms, and information about the databases searched, in your Appendix). Probably what’s most important is to show that your literature search, and write-up, weren’t just ad hoc. That is, that you didn’t just ‘cherry pick’ certain bits of literature, or arbitrarily select the papers from a five minute search of Google Scholar. However, you do it, you want to make it clear that you conducted a systematic, comprehensive, and meaningful review of the field: one that gave you the best chance of answering your own research question(s) to the fullest.

Study selection procedures

Generally, the best way to start finding articles for review is by setting out the different concepts within your study (for instance, as a table), and then brainstorming all the different terms that might be used to cover those concepts. For instance, if you were doing a review of research on person-centred therapy and autism, you might develop one set of terms for research (e.g., ‘empirical’, ‘study’, ‘evidence’…), one set for person-centred therapy (e.g., ‘person-centred’, ‘client-centred’, ‘client-centered’…), and one set for autism (e.g., ‘autism’, ‘asperger’s’, autistic…). To begin with, try and generate as many relevant terms as possible, and don’t forget that you want to include US-spelling as well as UK-spelling (like ‘person-centred’ and ‘person-centered’). Different search engines have different ‘wild cards’ that you can use (like * or $), which is where you specify just part of the word. For instance, if you want to search texts with ‘counselling’, ‘counsellor’, ‘counseling’, ‘counselor’, ‘counselled’, etc., you may be able to just use ‘counsel*’ (check the help sites on the specific search you are using). Importantly, you’ll also need to select the field that you want to search in. For instance, do you want to find sources with this term in the title, the abstract, or anywhere in the text—different field selections will give very different sets of results.

Below is an example of the search strategy that we used for our paper on interagency collaboration in child mental health services. You can see that we searched for terms about integration, and then also about children/young people, and mental issues. They needed to be post-1995 (and the study was conducted in 2015). The asterixes are wild cards that we used to ensure we didn’t miss terms with slightly different endings.

Example search strategy for review of integration in child mental health services

Although, ideally, this search strategy is set out before you do your search, it is inevitably going to be an iterative process: moving between testing out particular strategies, seeing how many hits you get, then revising the strategy to either broaden or narrow down the number of hits. For instance, you might start with a search that has ‘child*’ anywhere in the text, but because you get tens of thousands of hits, you revise this to require ‘child*’ to be in the title. As you start to see your hits, you may also want to include additional search terms for your concepts.

Very approximately, you want to find a search strategy that gets you, initially, something like 200 to 2000 hits. More than that becomes unmanageable. Less than that and you’re possibly missing some key articles. What you then do is to go through all the titles, or maybe the titles and abstracts, and identify just those that seem relevant to your review. Inevitably you’ll reject the majority of your hits: for instance, they might not be empirical papers, or they might use the term ‘person-centred’ to mean something entirely different from what you are looking at. That will then leave you with a smaller number of articles where you then might read through the whole paper to see if the article is relevant. Again, when you do that you’ll end up excluding a lot of your papers.

Ideally, particularly at Master’s and doctoral level, you should be keeping track of all the hits/articles you are reviewing and selecting/excluding at each stage. The ideal way to present that is through a Study flow diagram. Below is an example of such a diagram from our study of integration in child mental health services. You’ll see that there were a number of stages, and we explicitly state why we excluded certain papers. This level of detail may only be needed for doctoral or journal publishing level, but at any level you can use even a simple flow diagram to show key elements in the study selection process.

Example study flow diagram for review of integration in child mental health services

Just to add, at publishable level (and, ideally, at doctoral level), it’s good to be able to show some degree of ‘inter-rater reliability’ in the study selection process. What this means is that the selections made were not just down to the particularities of the individual researcher, but would be replicable across different researchers. The way that you do this is to have someone else (say a course colleague) do some of the selection process to, and then see how much similarity there was across selections. For instance, based on reading the full papers, what proportion of papers that you identified as eligible did a colleague also identify as eligible? If that’s less than, say, 50% or so, it suggests that there’s a lot of individual variation in what would be considered eligible for your review, and the criteria may need some tightening up.

If you know there are papers that are relevant to your review but aren’t coming up through your search strategy, that means there’s something wrong with the strategy. Have a look at why it’s not picking up those key papers and revise the strategy accordingly: if it’s missing those papers, it’s also possibly missing other papers that are important to your review. At the end of the day, saying ‘Well, I excluded Papers X and Y because they didn’t come up in my search strategy,’ isn’t enough. Your search strategy should be a tool for finding relevant texts, not the criteria, per se, of what is or is not relevant.

As well as using search engines, a key source to draw on is the reference list in the articles that you have found. Citation searches reverse that process, and can also be extremely helpful. In a citation search, you take key articles and then look at the subsequent articles that have referenced that article. That way, you find the very latest research related to that work. To do a citation search, you simply find the key article on a database and then click on the ‘citations’ link (or in Google Scholar, ‘Cited by…’). You can see this circled in red on the screenshot below:

Example ‘Cited by’ hyperlink in Google Scholar

By the end of this study selection process, you want to end up with somewhere between about five and 30-40 papers for inclusion in your review. More than that and you may well struggle to meaningfully integrate the findings. Less than that and your review is going to be more and more simply a re-statement of what the papers found. But if you’ve asked a really important, meaningful question, conducted a really thorough search, and then just found there isn’t anything out there—or only one or two studies—that can be a meaningful outcome in itself. Importantly, too, don’t take it as a sign of personal failure if you haven’t found any literature out there. The reality is, on a lot of counselling- and psychotherapy-related questions, there just isn’t much research. But identifying that can be really helpful in letting the field know areas to focus on for future.

Information sources

This may depend on the databases that your institution has access to. At minimum, you would ideally want to search Web of Science and PsychInfo, two of the principal sources for psychology-related papers. Google Scholar makes a useful addition to this: it can help you identify a different range of papers, more of the ‘grey’ literature. Don’t worry too much about your university or college library: that’s inevitably going to have a relatively limited array of books and journals.

How do I make my case?

As emphasised earlier, if you’re thinking, ‘How do I construct an argument so that I can show that I’ve got some good ideas here?’ you may be asking the wrong question for a literature review.  That’s fine for an introductory section of a thesis—showing why your question is of importance and relevance—but, as above, the aim of a literature review is to provide a balanced review of what we know so far in relation to a particular question, not to convince the reader of something.  So if the structure of your literature review goes something like, ‘Well x is really important, and so is y, and that means z is likely [and so I’m going to do some research now to show it is]’ you may need to backtrack.  Remember, ask yourself, ‘What is it that I don’t know that I am trying to find out?’  Trying to prove a point is never a great basis for a piece of research.

Format of the write-up

In most cases in the counselling and psychotherapy field, reviews will be of a qualitative nature (i.e., written up in words)—and that’s what I’ll address here. There are also reviews that mathematically combine data, known as meta-analysis. These have their own particular methods (see, for instance, Practical meta-analysis) and are best conducted using dedicated software, such as Comprehensive Meta-analysis.

Use headings and subheadings in each of the sections to keep a clear structure to the paper, and make sure that the hierarchy of these headings is clear to the reader: i.e., make the higher level headings bigger, bolder, etc. as compared with lower order headings. Some pointers on formatting and presenting your work are available here.

You will probably want to start your literature review with a short section detailing the method by which you went about your literature search. Even if you didn’t use a systematic method throughout, it’s worth saying something of how you searched the literature, so that the reader has a sense of what you might have found—and missed.

A table of the final articles that you included in your review can be really helpful, either at the start of the review or as an appendix. Each paper can be a row, and then you can have various key features in the columns, such as the location of the study, the number of participants, key findings, etc. An example—the first few rows from our review of integration in child mental health services—is below.

Example table of studies for review of integration in child mental health services

Try to avoid ‘laundry list’ reviews: ‘stringing together sets of notes on relevant papers’ (McLeod, 1994, p.20) one after another.  For instance:

• Smith (1992) found that…..

• And Brown (2011) found that…

• And Jones (1996) found that…

• And then Patel et al. (2001) found that…

Or narrative/historical version of a laundry list review: For instance:

• First, Smith (1992) found that…..

• Then Jones (1996) found that…

• Then Patel et al. (2001) found that…

• Then Brown (2011) found that…

Remember that, particularly at Master’s and doctoral level, a literature review is not just about précising previous research in the field: providing summaries of what lots of different studies said.  It’s about drawing the research together in coherent and meaningful ways.

So wherever possible, adopt a thematic style of review.  ‘This strategy involves the identification of distinct issues or questions that run through the area of research under consideration. Thematic literature reviews enable the writer to create meaningful groupings of papers in different aspects of a topic.  This is therefore a highly flexible style of review, in which the complex nature of work in an area of area can be respected while at the same time bringing some degree of order and organisation to the material’ (McLeod, 1994, p.20).  In a thematic review, it is likely that several different sources will be cited in one paragraph.

• Some research has shown A… (Jones, 1996; Smith, 1992)

• But other research has shown B (Patel et al., 2001; Jones, 1996), although there are some problems with these findings (Grey et al., 1990).

• More broadly, we know that Z… (White and Brown, 2001; Yellow, 2010).

• And there is also some research to suggest X (Blue, 2003; Grey, 1994).

• What we know so far, then, is that A seems very likely, and that is supported by Z and X, though B raises some problems about this.  

When you review the literature, you don’t need to ascribe every study equal weight and space.  Indeed, if you are, it probably suggests you’re being too descriptive and not discriminating enough.  Some of the studies you look at will be spot-on relevant to your own research, some only tangentially so.  So if you’re extracting what’s really most meaningful to your own questions, you should be taking a lot more from some sources than others.  You’re not reviewing to make all these authors feel like they’re being paid due regard.  You’re reviewing to take what you need from their work to say what we currently know in relation to your question(s).  If content isn’t relevant, leave it out.  If it’s highly relevant, say a lot about it.

A thematic approach really allows you to show a high-level, synthesised understanding.

Whenever you make claims about how things are (for instance, ‘empathy is a key factor in therapeutic outcomes’), you must always provide some reference for this.

Make sure you explicitly state somewhere, either at the end of the literature review or in your design, what the main aims/objectives of your study are, and, if relevant, your hypothesis/hypotheses.

Wherever possible, go back to the original sources and reference those, rather than ‘cited in….’  Citations never looks great—that you haven’t bothered to consult the original sources.  If you really can’t access the original source (e.g., it’s in another language, or out of publication and unavailable), that’s fine, but use citations sparingly.  And be really careful not to take references from a secondary source and cite them as if you have read them: find out what the original authors really said.

EVIDENCE or theory?

Your literature review might be of evidence in relation to a particular question: for instance, ‘How do clients experience person-centred therapy?’ Alternatively, it might be of theoretical propositions: for instance, ‘What is a relational psychodynamic theory of development?’ It could also combine evidence and theory, for instance, ‘What is the relationship between alliance and outcomes for young people?’ There’s no right or wrong here—it is entirely dependent on your question.

What is important, however, is to be clear about when you’re reviewing theory and when you’re reviewing evidence. So, when you write up your review, try not to mix up theoretical statements like, ‘Rogers hypothesised that….’ with empirical statements like, ‘Greenberg et al. found that…’ What someone thinks (even if it was Carl Rogers!), and what someone actually found, are quite separate things. So if you are covering both in your review, it may be an idea to write them up as separate sections.

Just to note, also be careful about mixing up primary studies (e.g., specific pieces of empirical research), with reviews or ‘meta-analyses’ of the field. For instance, you may find through your search strategies a number of papers which review primary studies in relation to a particular question. That’s great, but then use that review to identify the primary studies, and include or exclude those primary studies in your review, as appropriate. You could then note the reviews papers in your introduction, and say about how your review is different. Alternatively, you could do a review of reviews in a field—if there’s a logic in bringing them together and it would be redundant to replicate the review process. But, again, don’t mix that up with a review of primary studies—do one or the other, and be clear about which it is.

The 'target' approach to structuring your literature review

One way to think about structuring your literature review is like a ‘target’. Start with the evidence that is most relevant to your research question (and perhaps do a systematic review of it). Then what else might be most closely relevant? For instance, if you’re doing a study on negative experiences of young people in person-centred therapy, you’d want to start by looking comprehensively for everything on that specific question. But if there’s not much, then you could review the research on negative experiences of young people in other therapies, then negative experiences of adults in person-centred therapy. The more literature there is at the ‘bullseye’ of your target, the less you need to go broader. But if there’s really not much (and that’s fine), then broaden out to literature from which we might be able to extrapolate potential answers to your question(s).

Target approach to writing up a literature review

The ‘pyramid’ approach to structuring your literature review

Another common approach is the pyramid one, where you start with the broadest area of literature on your topic, and then narrow downwards to more specific knowledge leading on to your research question.

Pyramid approach to writing up a literature review

Summary

Ultimately, a literature review is not about showing that you are smart and know things, or that you can follow a pre-specified methodology.  It’s about drawing on all your knowledge and skills to present your best understanding of the answers to your question(s), to date. 

You are to become the master in this field. And your reader is looking to you to give them an informed, rigorous, and up to date understanding. Sometimes, the hardest bit of doing a literature review is feeling the confidence to be able to do that (see my blog on the Research mindset). But you can, providing you choose your scope and your methods wisely.

Further reading

There are several texts on how to write a literature review, relevant to the counselling and psychotherapy field. Torgerson’s Systematic reviews is a good general introduction. 7 steps to a comprehensive literature review has been recommended to me, and there is the popular Doing a literature review in health and social care. John McLeod’s classic Doing research in counselling and psychotherapy gives some excellent guidance on reading the literature (Chapter 2).

Acknowledgements

Photo by Jakirseu, CC BY-SA 4.0

Disclaimer

The information, materials, opinions, or other content (collectively Content) contained in this blog have been prepared for general information purposes. Whilst I’ve endeavoured to ensure the Content is current and accurate, the Content in this blog is not intended to constitute professional advice and should not be relied on or treated as a substitute for specific advice relevant to particular circumstances. That means that I am not responsible for, nor will be liable for any losses incurred as a result of anyone relying on the Content contained in this blog, on this website, or any external internet sites referenced in or linked in this blog.

Choosing Your Research Topic: Some Pointers

If you're doing a research project in counselling, psychotherapy, or counselling psychology, choosing your topic can be one of the hardest things to get right. And often one of the things you get the least advice on. So how should you go about it?

Read through previous counselling/psychotherapy/counselling psychology research theses

Invaluable! Essential! Probably the most useful thing you can do to get you started. This will give you a real sense of the ‘shape’ of a research study in this field, what is expected of you, and the kinds of questions that you might want to ask.  Should be in your college library or ask a tutor.

originalITY is not everything

Often, in my experience, students come into Master’s or doctoral research projects thinking, ‘I must do something original… I must do something original.’ So they work away at finding some dark corner somewhere that no-one has ever looked into before. Of course, there does need to be originality in your research, but if you’re burrowing away into a corner somewhere then there’s a real danger that no-one else is going to be particularly interested in where you’re going—you’re off into a world of your own. So instead of asking yourself, ‘What can I do that no-one else has ever done before?’ ask yourself, ‘What can I do that builds on what has been done before?’ And that means…

…Get a sense of the field

What are the key questions being asked in your field today?  What are the issues that matter and that are of relevance to practice?  It’s great to draw on your own interests and experiences, but also make sure you develop some familiarity with the field as it currently stands.  This will help to ensure that your research is topical and relevant—of interest and importance to the wider field as well as yourself.  A great thing to do can be to find out what your tutors are researching and what they see as the key issues in the current field.  And do remember that there may be the possibility of developing your project alongside them in some way, so that you can contribute to a particular national- or international-level research initiative.

Also, right from the start, think about how your work and your research question might have the capacity to influence practice and policy.  This may be the biggest research project you’ll ever do.  So make it count.  Think about doing something that can really help others learn how to improve their practice, perhaps with a particular group of clients, or with respect to a particular method.  If it’s a doctoral level project, you’ll become a leading expert in that field, and you’ll be in a position to teach the rest of us how to be more helpful.  So think about what you’d like to find out about, which you can then disseminate to the field as a whole.

If you want to make your research count, have a really long think before you dive into doing research on therapists’ experiences or perceptions.  Lots of students study this: it’s reflexive, and it’s a relatively easy group to access.  But it also raises the question of how interested people are really going to be in how therapists’ see things.  After all, we’ve all been trained in particular beliefs and assumptions, so if we’re the subject of research, we’re often just going to reiterate what we’ve been taught to think.  Generally, clients make a much more worthwhile participant group, because you’re hearing first hand what it’s really like in therapy, and what works and what doesn’t.

Consult the literature

Once you’ve got some idea of what you’d like to look at, find out how other people have tried to answer that question. If no-one has tried to answer it before, that’s great, but you need to be really sure about that before going on to furrow your own path—after all, you don’t want to get to the end of your research to find out that somebody ‘discovered’ the same thing as you decades ago. So have a look on Google Scholar, and particularly on social science search engines like PsychInfo. Undertaking such searches also ensures that your research will be embedded within the wider research field, and it may well give you ideas about the kinds of questions that are timely to ask.

Make sure it's related to therapeutic practice

Choose a topic which is related, at least in some way, to the field of therapeutic practice. Most directly, this may include things like: clients’ experiences of helpful and unhelpful factors, how psychological interventions are perceived from those outside the field, or the applied role of counselling in such fields as education. Exploring people’s experiences of a particular phenomenon—for instance, women’s experiences of birth trauma—can also be related to therapeutic practice, but just be clear what the association might be. For instance, could that help therapists know how to work most effectively with that client group, or to know what issues to be sensitized to.

Find yourself a clearly-defined question

Try to find a single, clearly defined question as the basis for your study (see my Research Aims and Questions pointers). This can then serve as your title. If you can't encapsulate your research project into a single question/sentence at some point, the chances are, you're probably not clear about exactly what it is you are asking.

That's ‘question’, not ‘questions’

One of the biggest problems students face is that they ask too many inter-related questions, with too many constructs of interest, and therefore get very muddled in what they are doing. For instance, they’re interested in attachment styles, and how it relates to dropout as mediated by the client’s personality in EMDR for trauma. But that’s five different constructs (attachment styles, dropout, personality types, EMDR, trauma—and, indeed, a sixth implicit one, which is the outcomes of EMDR for trauma), and generally you want to focus down on just one or two constructs (particularly in qualitative research), or maybe three at most if you are doing quantitative. So, for instance, you could focus on how attachment style influences dropout, or how clients experience EMDR for trauma, or the role of personality styles in mediating outcomes in EMDR for trauma. Or you could even just focus down on how clients experience dropout. All nice, straightforward questions that you can really get into at Master’s or doctoral level depth. So think about the constructs that you definitely want to focus in on, and let go of those that are maybe less central to your concerns. Of course, that’s difficult, and three of the main reasons why are given below—along with the things you may need to remind yourself of:

'I won't have enough material otherwise.'  Your word limit may seem like a lot, but you'll be amazed at how quickly it goes. If you just focus on one question, you will be able to go into it in a great amount of depth—far more appropriate to Master’s or doctoral study than trying to answer a number of questions and subsequently coming away with numerous superficial answers.

'There's lots of different aspects of this area that I'm interested in.' That's great, but you won't be able to cover it all in this one project. You can always do further research after this one. In limiting yourself to just one question, you may well experience feelings of loss or disappointment as you let go of areas you're really interested in, but it's better to feel that loss now than after you've put months of work into areas that are just too dispersed.

'I've already started to ask this other question, and I don't want to lose the reading that I've already done'. Again, it can be painful letting go of things, but there is no value in ‘throwing good money after bad.’ Sometimes in research you need to be brutal, and cut out areas of inquiry that don't fit in—even if you've sweated blood over them. Remember what authors say: the quality of their book is defined by what they leave out!

That’s ‘question’, not ‘answer’

Some of the most problematic projects come about when researchers try to show that a particular answer is the correct one, and consequently won’t let anything—including their own findings—get in their way. So if you really believe something about psychological therapies, like ‘person-centred therapy is much more effective than cognitive-behavioural therapy’, or ‘women make much better counselling psychologists than men’ then you may want to steer clear of this topic. That is, unless you can really get yourself into a frame of mind in which you are open to the possibility that you might find the absolute opposite of what you want—and you can enthusiastically write about the implications of this finding. Good research is like good therapy: you put to one side your own assumptions as much as possible, so that the reality of whatever you are encountering can come through. So, in trying to work out your research question, here’s something to really ask yourself:

What is the question that I genuinely don’t know the answer to (but would love to find out)?

And ‘genuinely’ here means genuinely. It means you really, actually, don’t know what the answer to that question is. If you can find that question, it’ll help enormously in your whole research project, because it’ll mean that you’re genuinely open to, and interested in, finding out what’s out there. That’s research!

But make sure there’s not too much literature on it

If you ask a question on which much has already been written—like the effectiveness of person-centred therapy—then you’re likely to be drowned in material before you even get to the end of the literature review. So narrow down your question—e.g. the effectiveness of advanced empathy in person-centred therapy—until you’ve got a manageable number of references in your sights. Don’t worry if it seems too few, you’ll no doubt pick up more references as you go along. And remember, you need to have full mastery of the literature regarding the question your asking, and it is a lot easier to master the information in five or six papers than it is in hundreds.

What’s often ideal is if you can move one step on from some pre-existing literature: e.g. extending a study about depression in men to looking at depression in women, testing out a theory that you’ve found in a book, or using qualitative research to address a question that has previously only been addressed through quantitative research. So don’t get too hung up on being totally ‘original’: in fact, if you try to be too original you can end up in a sea of confusion with no theoretical or methodological concepts to anchor yourself to. Having an original twist is often much more productive—you’re saying something new, but you’re building on what’s already been laid down.

Think methodology from the start

It’s no good coming up with a brilliant question if there is no way of actually answering it, or if answering it is going to be such a headache that you’ll wish that you never started in the first place. So as you come up with ideas, think about how feasible it might actually be to put them into practice. This is something you may really want to discuss early on with a colleague or research tutor.

Respondents MUST be accessible

In terms of the feasibility of the study, probably the most important question is whether or not you are actually going to get anyone to participate—to respond to your interviews, questionnaires, etc. It is essential to the success of your study that you get a good response rate, so thinking about who you do research with is often as important as thinking about what you do (see my research pointers here on recruiting participants). A number of factors will determine how good your response is likely to be: how big the population is in total, their motivation to help you, how easy it will be for you to get in touch with them, how cautious you will need to be as a consequence of ethical safeguards. So don’t just come up with an idea and hope blindly that someone out there will be interested. However hard you think it will be to get participants, you can guarantee that it will actually be several times harder than that, so make sure this is something you think about, and address, at an early stage.

Ethics come first

The principles of non-maleficence—doing no harm to your respondent—and, ideally, beneficence—promoting the respondent’s well-being—should be an integral part of your research design. So, right from the very start of your project, think about ways in which your research might benefit those that are involved; and also make sure that you have read and familiarised yourself with appropriate ethical guidelines, as well as any other sets of relevant standards.

Aside from ‘doing the right thing’, the issue of ethics will be an important one for you because, in any research study, you will need to submit your project to an ethics committee (see above), and the more sensitive your work, the more committees and the longer the time this is likely to take. For instance, if you wish to carry out research in the National Health Service, you will almost certainly need to go through an NHS ethics committee, which can take many months to consider and respond to proposals. So, as you start to develop your research ideas, be aware of the ethical issues and processes that it might raise, and try to find out about the ethical submissions that such a study is likely to entail. That way, you won’t suddenly find yourself facing a long and uncertain wait before you can proceed with your work -- or, if you do, at least you’ll be prepared for it.